题目内容
在△ABC中,已知tan
=sinC,给出以下四个论断:
①tanA•cotB=1,
②1<sinA+sinB≤
,
③sin2A+cos2B=1,
④cos2A+cos2B=sin2C,
其中正确的是( )
| A+B |
| 2 |
①tanA•cotB=1,
②1<sinA+sinB≤
| 2 |
③sin2A+cos2B=1,
④cos2A+cos2B=sin2C,
其中正确的是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
∵tan
=sinC
∴
=2sin
cos
整理求得cos(A+B)=0
∴A+B=90°.
∴tanA•cotB=tanA•tanA不一定等于1,①不正确.
∴sinA+sinB=sinA+cosA=
sin(A+45°)
45°<A+45°<135°,
<sin(A+45°)≤1,
∴1<sinA+sinB≤
,
所以②正确
cos2A+cos2B=cos2A+sin2A=1,
sin2C=sin290°=1,
所以cos2A+cos2B=sin2C.
所以④正确.
sin2A+cos2B=sin2A+sin2A=2sin2A=1不一定成立,故③不正确.
综上知②④正确
故选B.
| A+B |
| 2 |
∴
sin
| ||
cos
|
| A+B |
| 2 |
| A+B |
| 2 |
整理求得cos(A+B)=0
∴A+B=90°.
∴tanA•cotB=tanA•tanA不一定等于1,①不正确.
∴sinA+sinB=sinA+cosA=
| 2 |
45°<A+45°<135°,
| ||
| 2 |
∴1<sinA+sinB≤
| 2 |
所以②正确
cos2A+cos2B=cos2A+sin2A=1,
sin2C=sin290°=1,
所以cos2A+cos2B=sin2C.
所以④正确.
sin2A+cos2B=sin2A+sin2A=2sin2A=1不一定成立,故③不正确.
综上知②④正确
故选B.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.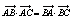 .
. |=|
|=| |;
|; ,求|
,求| -t
-t