题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)
【解析】试题分析:(1)先根据导数几何意义得![]() ,解得实数
,解得实数![]() 的值;(2)设
的值;(2)设![]() ,构造函数
,构造函数![]() ,则转化为
,则转化为![]() 在
在![]() 上为增函数,即得
上为增函数,即得![]() 在
在![]() 上恒成立,参变分离得
上恒成立,参变分离得![]() ,最后根据二次函数最值求实数
,最后根据二次函数最值求实数![]() 的取值范围;(3)先化简不等式,并构造函数
的取值范围;(3)先化简不等式,并构造函数![]() ,求导数,按导函数零点与定义区间大小关系讨论函数单调性,根据单调性确定函数最小值,根据最小值小于零解得实数
,求导数,按导函数零点与定义区间大小关系讨论函数单调性,根据单调性确定函数最小值,根据最小值小于零解得实数![]() 的取值范围.
的取值范围.
试题解析:解:(1)由![]() ,得
,得![]() .
.
由题意, ![]() ,所以
,所以![]() .
.
(2)![]() .
.
因为对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,设
恒成立,设![]() ,则
,则![]() 即
即![]() 恒成立.
恒成立.
问题等价于函数![]() ,
,
即![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() 在
在![]() 上恒成立.即
上恒成立.即![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.
(3)不等式![]() 等价于
等价于![]() ,整理得
,整理得![]() .构造函数
.构造函数![]() ,
,
由题意知,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() .
.
![]() .
.
因为![]() ,所以
,所以![]() ,令
,令![]() ,得
,得![]() .
.
①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增.只需
上单调递增.只需![]() ,解得
,解得![]() .
.
②当![]() 即
即![]() 时,
时, ![]() 在
在![]() 处取最小值.
处取最小值.
令![]() 即
即![]() ,可得
,可得![]() .
.
令![]() ,即
,即![]() ,不等式
,不等式![]() 可化为
可化为![]() .
.
因为![]() ,所以不等式左端大于1,右端小于等于1,所以不等式不能成立.
,所以不等式左端大于1,右端小于等于1,所以不等式不能成立.
③当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,只需
上单调递减,只需![]() ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是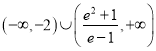 .
.

【题目】某同学学习习惯不好,把黑板上老师写的表达式忘了,记不清楚是![]() 还是
还是![]() .翻出草稿本发现在用五点作图法列表作图时曾算出过一些数据(如下表).
.翻出草稿本发现在用五点作图法列表作图时曾算出过一些数据(如下表).
| 0 |
|
|
| |
|
|
|
|
| |
| 0 | 3 | 0 | 0 |
(1)请你帮助该同学补充完表格中的数据,写出该函数的表达式![]() ,并写出该函数的最小正周期;
,并写出该函数的最小正周期;
(2)若利用![]() 的图象用图象变化法作
的图象用图象变化法作![]() 的图象,其步骤如下:(在空格内填上合适的变换方法)
的图象,其步骤如下:(在空格内填上合适的变换方法)
第一步:![]() 的图象向右平移
的图象向右平移![]() _____得到
_____得到![]() _____的图象;
_____的图象;
第二步:![]() 的图象(纵坐标不变)______得到
的图象(纵坐标不变)______得到![]() _____的图象;
_____的图象;
第三步:![]() 的图象(横坐标不变)_____得到
的图象(横坐标不变)_____得到![]() 的图象.
的图象.

