题目内容
设O是平行四边形ABCD的两条对角线的交点，下列向量组：
（1）
与
；
（2）
与
；
（3）
与
；
（4）
与
，
其中可作为这个平行四边形所在平面表示它的所有向量的基底的向量组可以是______．
（1）
| AD |
| AB |
（2）
| DA |
| BC |
（3）
| CA |
| DC |
（4）
| OD |
| OB |
其中可作为这个平行四边形所在平面表示它的所有向量的基底的向量组可以是______．
如下图所示：
（1）
与
不共线，故（1）可作为这个平行四边形所在平面表示它的所有向量的基底；
（2）
与
共线，故（2）不可作为这个平行四边形所在平面表示它的所有向量的基底；
（3）
与
不共线，故（3）可作为这个平行四边形所在平面表示它的所有向量的基底；
（4）
与
共线，故（4）不可作为这个平行四边形所在平面表示它的所有向量的基底；
故答案为：（1），（3）
（1）
| AD |
| AB |
（2）
| DA |
| BC |
（3）
| CA |
| DC |
（4）
| OD |
| OB |
故答案为：（1），（3）
练习册系列答案
相关题目
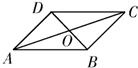如图，设O是平行四边形ABCD的两条对角线AC，BD的交点，下列向量组：