题目内容

设O是平行四边形ABCD的两条对角线AC与BD的交点，对于下列向量组：①
AD
与
AB
；②
DA
与
BC
；③
CA
与
DC
；④
OD
与
OB
．其中能作为一组基底的是
①③
①③
（只填写序号）．
分析：利用基底的定义，平面内任意两个不共线的向量都可以作为基底，故需判断各个选项中的两个向量是否共线．
解答：解析：由于①
AD
与
AB
不共线，③
CA
与
DC
不共线，所以都可以作为基底．
②
DA
与
BC
共线，④
OD
与
OB
共线，不能作为基底．
故答案为：①③．
点评：本题考查平面向量基本定理及其意义，基底的定义．
练习册系列答案
相关题目
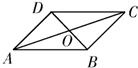精英家教网如图，设O是平行四边形ABCD的两条对角线AC，BD的交点，下列向量组：
①
AD
与
AB
；②
DA
与
BC
；
③
CA
与
DC
；④
OD
与
OB
．
其中可作为这个平行四边形所在平面的一组基底的是．
A、①②B、③④C、①③D、①④
设O是平行四边形ABCD的两条对角线的交点，下列向量组：
（1）
AD
与
AB
；
（2）
DA
与
BC
；
（3）
CA
与
DC
；
（4）
OD
与
OB
，
其中可作为这个平行四边形所在平面表示它的所有向量的基底的向量组可以是
（1），（3）
（1），（3）
．
设O是平行四边形ABCD的两条对角线AC与BD的交点，对于下列向量组：①
AD
与
AB
；②
DA
与
BC
；③
CA
与
DC
；④
OD
与
OB
．其中能作为一组基底的是______（只填写序号）．
设O是平行四边形ABCD的两条对角线的交点，下列向量组：
（1）
AD
与
AB
；
（2）
DA
与
BC
；
（3）
CA
与
DC
；
（4）
OD
与
OB
，
其中可作为这个平行四边形所在平面表示它的所有向量的基底的向量组可以是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网