题目内容
已知函数f(x)=ax-lnx(a为常数).
(Ⅰ)当a=1时,求函数f(x)的最小值;
(Ⅱ)求函数f(x)在[1,+∞)上的最值;
(Ⅲ)试证明对任意的n∈N﹡都有 <1.
<1.
【答案】
解(1)当 时,函数
时,函数 =
=
 ,
,
∵ ,令
,令 得
得
∵当 时,
时, ∴函数
∴函数 在
在 上为减函数
上为减函数
∵当 时
时 ∴函数
∴函数 在
在 上为增函数
上为增函数
∴当 时,函数
时,函数 有最小值,
有最小值, --------3分
--------3分
(2)∵
若 ,则对任意的
,则对任意的 都有
都有 ,∴函数
,∴函数 在
在 上为减函数
上为减函数
∴函数 在
在 上有最大值,没有最小值,
上有最大值,没有最小值, ; --------4分
; --------4分
若 ,令
,令 得
得
当 时,
时, ,当
,当 时
时 ,函数
,函数 在
在 上为减函数
上为减函数
当 时
时 ∴函数
∴函数 在
在 上为增函数
上为增函数
∴当 时,函数
时,函数 有最小值,
有最小值, ------6分
------6分
当 时,
时, 在
在 恒有
恒有
∴函数 在
在 上为增函数,
上为增函数,
函数 在
在 有最小值,
有最小值, . ---------7分
. ---------7分
综上得:当 时,函数
时,函数 在
在 上有最大值,
上有最大值, ,没有最小值;
,没有最小值;
当 时,函数
时,函数 有最小值,
有最小值, ,没有最大值;
,没有最大值;
当 时,函数
时,函数 在
在 有最小值,
有最小值, ,没有最大值.---8分
,没有最大值.---8分
(3)由(1)知函数 =
= 在
在 上有最小值1
上有最小值1
即对任意的 都有
都有 ,即
,即 , ---------10分
, ---------10分
当且仅当 时“=”成立
时“=”成立
∵ ∴
∴ 且
且
∴

∴对任意的 都有
都有 . ……12分
. ……12分
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 -x (e为自然对数的底数).
-x (e为自然对数的底数). ≤x≤2}且M∩P≠
≤x≤2}且M∩P≠ ,求实数a的
,求实数a的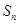 =
= (t为常数,t≥0),是否存在等比数列{
(t为常数,t≥0),是否存在等比数列{ },使得b1+b2+…
},使得b1+b2+… 与x=1时都取得极值。
与x=1时都取得极值。