题目内容
已知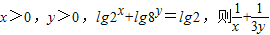 的最小值是 .
的最小值是 .
【答案】分析:由对数的运算性质,lg2x+lg8y=lg2x+lg23y=(x+3y)lg2,结合题意可得,x+3y=1;再利用1的代换结合基本不等式求解即可.
解答:解:lg2x+lg8y=lg2x+lg23y=(x+3y)lg2,
又由lg2x+lg8y=lg2,
则x+3y=1,
进而由基本不等式的性质可得,
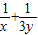 =(x+3y)(
=(x+3y)( 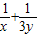 )=2+
)=2+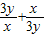 ≥2+2=4,
≥2+2=4,
当且仅当x=3y时取等号,
故答案为:4.
点评:本题考查基本不等式的性质与对数的运算,注意基本不等式常见的变形形式与运用,如本题中,1的代换.
解答:解:lg2x+lg8y=lg2x+lg23y=(x+3y)lg2,
又由lg2x+lg8y=lg2,
则x+3y=1,
进而由基本不等式的性质可得,
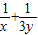 =(x+3y)(
=(x+3y)( 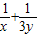 )=2+
)=2+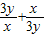 ≥2+2=4,
≥2+2=4,当且仅当x=3y时取等号,
故答案为:4.
点评:本题考查基本不等式的性质与对数的运算,注意基本不等式常见的变形形式与运用,如本题中,1的代换.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
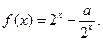 将
将 的图象向右平移2个单位,得到
的图象向右平移2个单位,得到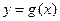 的图象.
的图象.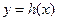 与函数
与函数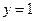 对称,求函数
对称,求函数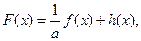 已知
已知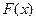 的最小值是
的最小值是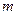 ,且
,且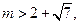 求实数
求实数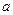 的
的 取值范围.
取值范围. 的最小值是5,则z的最大值 .
的最小值是5,则z的最大值 . 的最小值是
的最小值是 ,则二项式
,则二项式 展开式中
展开式中 项的系数为( )
项的系数为( ) B.
B.  C.
C. D.
D. 
 的最小值是
的最小值是 B.2 C.3 D.4
B.2 C.3 D.4 的最小值是( )
的最小值是( )  C.4 D.2
C.4 D.2