题目内容
如图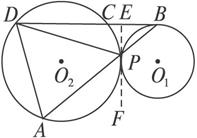
图
求证:AD2+BC·BD=AB2.
解析:由BC·BD联想到割线定理BC·BD=BP·AB,又等式右边含AB2,考虑移项后和差化积.
AD2=AB2-BC·BD=AB2-BP·AB
=AB(AB-BP)=AB·AP.
只需证AD2=AB·AP,利用△ABD∽△ADP.
证明:过P作公切线EF交BD于点E,
由切线长定理,得EB=EP.
∴∠B=∠EPB.∵∠EPB=∠APF,∠APF=∠ADP.
∴∠B=∠ADP.
又∠A=∠A,∴△ABD∽△ADP.
∴![]() =
=![]() .
.
∴AD2=AB·AP.
由割线定理,得BC·BD=BP·AB.
∴AD2+BC·BD=AB·AP+BP·AB=AB(AP+BP)=AB2.
∴AD2+BC·BD=AB2.

练习册系列答案
相关题目
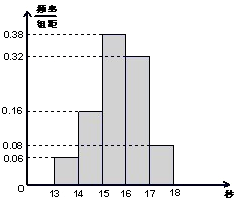 某班50名学生在一次百米测试中,成绩全部介于13~18秒之间,将测试结果分成五组:第一组[13,14),经二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图,若成绩大于或等于14秒且小于16秒认为良好.
某班50名学生在一次百米测试中,成绩全部介于13~18秒之间,将测试结果分成五组:第一组[13,14),经二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图,若成绩大于或等于14秒且小于16秒认为良好.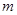 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为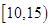 ,
,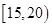 ,
,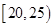 ,
,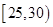 ,
,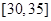 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在
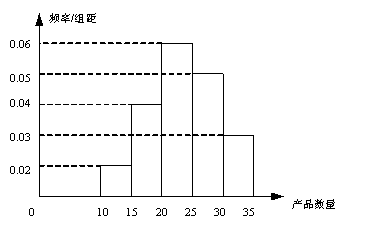 人不在同一组的概率是多少?
人不在同一组的概率是多少?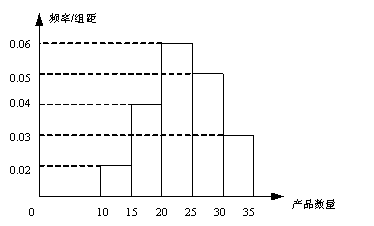 人不在同一组的概率是多少?
人不在同一组的概率是多少?