题目内容
选做题(选修4—1:几何证明选讲)如图,△ABC是圆O的内接三角形,AC=BC,D为圆O中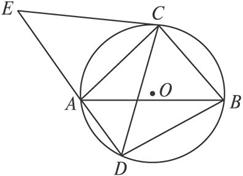
(1)求证:AE=BD;
(2)若AC⊥BC,求证:AD+BD=![]() CD.
CD.
证明:(1)在△ABC中,∠CAB=∠CBA.在△ECD中,∠CED=∠CDE.
∵∠CBA=∠CDE,∴∠ACB=∠ECD.∴∠ACB-∠ACD=∠ECD-∠ADE.
∴∠ACE=∠BCD.
在△ACE和△BCD中,∠ACE=∠BCD;CE=CD;AC=BC,∴△ACE≌△BCD.∴AE=BD.
(2)若AC⊥BC,∵∠ACB=∠ECD,∴∠ECD=90°,∠CED=∠CDE=45°.
∴DE=2CD.又∵AD+BD=AD+EA=ED,∴AD+BD=2CD.

练习册系列答案
相关题目

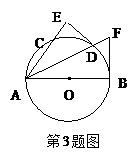 (选做题)选修4-1:几何证明选讲
(选做题)选修4-1:几何证明选讲
 如图,圆
如图,圆