题目内容
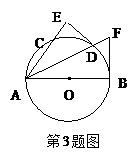
选做题(选修4—1:几何证明选讲)如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=2![]() ,AE=6
,AE=6![]() ,求EC的长.
,求EC的长.
解:(1)证明:取BD的中点O,连结OE.
∵BE平分∠ABC,∴∠CBE=∠OBE.又∵OB=OE,
∴∠OBE=∠BEO.∴∠CBE=∠BEO.∴BC∥OE.
∵∠C=90°,∴OE⊥AC.∴AC是△BDE的外接圆的切线.
(2)设⊙O的半径为r,则在△AOE中,
OA2=OE2+AE2,即(r+2![]() )2=r2+(6
)2=r2+(6![]() )2,解得r=26.
)2,解得r=26.
∴OA=2OE.∴∠A=30°,∠AOE=60°.∴∠CBE=∠OBE=30°.
∴EC=![]() BE=
BE=![]() ×
×![]() r=
r=![]() ×
×![]() ×2
×2![]() =3
=3![]() .
.

练习册系列答案
相关题目

 (选做题)选修4-1:几何证明选讲
(选做题)选修4-1:几何证明选讲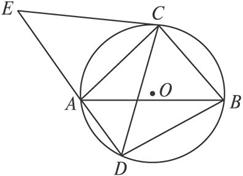
 如图,圆
如图,圆