题目内容
已知数列(1)判断![]() 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)求数列![]() 的通项an;
的通项an;
(3)若bn=2(1-n)an,求f(n )=![]() 的最大值及取最大值时n的值.
的最大值及取最大值时n的值.
答案:
解析:
解析:
| (1)∵ n³2时,an=Sn-Sn-1,又an+2SnSn-1=0
∴ Sn-Sn-1=--2SnSn-1,即 ∴ 由S2=a1+a2= ∵ a1+a3¹2a2,∴ (2)∵ n³2时, (3)∵ b1=0,n³2时,bn=2(1-n)an= ∴ 故当n=1时,f(n)取得最大值
|

练习册系列答案
相关题目
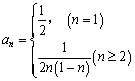
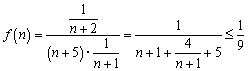 ,当且仅当n=1时取等号.
,当且仅当n=1时取等号. 求使不等式
求使不等式 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为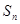 ,且
,且 ,
, ,并猜想
,并猜想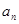 的表达式。
的表达式。