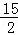题目内容
幂指函数y=f(x)g(x)在求导数时,可以运用对数法:在函数解析式两边求对数得 ,两边求导数得
,两边求导数得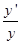 =
= ,于是y′=f(x)g(x)·
,于是y′=f(x)g(x)· .运用此法可以探求得知y=
.运用此法可以探求得知y= 的一个单调递增区间为( ).
的一个单调递增区间为( ).
| A.(0,2) | B.(2,3) | C.(e,4) | D.(3, 8) |
A
解析试题分析:由题可知对原函数两边取对数可得 ,两边对
,两边对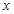 求导可得
求导可得 ,即
,即 ,对于
,对于 时,
时, ,
, ,
, ,故
,故 ,为单调递增区间.
,为单调递增区间.
考点:导数的运算.

练习册系列答案
相关题目
已知函数 .那么不等式
.那么不等式 的解集为( ).
的解集为( ).
A. | B. |
C. | D. |
已知 ,
, ,
, ,则( )
,则( )
A. | B. | C. | D. |
已知 ,且
,且 ,
,
成等比数列,则xy( )
| A.有最大值e | B.有最大值 |
| C.有最小值e | D.有最小值 |
对任意a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,则x的取值范围是 ( )
| A.1<x<3 | B.x<1或x>3 |
| C.1<x<2 | D.x<1或x>2 |
某种商品进价为每件100元,按进价增加25%出售,后因库存积压降价,按九折出售,每件还获利( )
| A.25元 | B.20.5元 | C.15元 | D.12.5元 |
(2014·嘉兴模拟)已知a= ,b=0.3-2,c=lo
,b=0.3-2,c=lo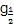 2,则a,b,c的大小关系是( )
2,则a,b,c的大小关系是( )
| A.a>b>c | B.a>c>b | C.c>b>a | D.b>a>c |
 的图象大致为( )
的图象大致为( )