题目内容
已知椭圆C的对称中心为坐标原点O,焦点在![]() 轴上,左右焦点分别为
轴上,左右焦点分别为![]() ,且
,且![]() =2
=2![]() ,点
,点![]() 在该椭圆上。
在该椭圆上。
(1)求椭圆C的方程;
(2)设椭圆C上的一点![]() 在第一象限,且满足
在第一象限,且满足![]() ,圆
,圆![]() 的方程为
的方程为![]() .求点
.求点![]() 坐标,并判断直线
坐标,并判断直线![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(3)设点![]() 为椭圆的左顶点,是否存在不同于点
为椭圆的左顶点,是否存在不同于点![]() 的定点
的定点![]() ,对于圆
,对于圆![]() 上任意一点
上任意一点![]() ,都有
,都有![]() 为常数,若存在,求所有满足条件的点
为常数,若存在,求所有满足条件的点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
已知椭圆C的对称中心为坐标原点O,焦点在![]() 轴上,左右焦点分别为
轴上,左右焦点分别为![]() ,且
,且![]() =2
=2![]() ,点
,点![]() 在该椭圆上。
在该椭圆上。
(1)求椭圆C的方程;
(2)设椭圆C上的一点![]() 在第一象限,且满足
在第一象限,且满足![]() ,圆
,圆![]() 的方程为
的方程为![]() .求点
.求点![]() 坐标,并判断直线
坐标,并判断直线![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(3)设点![]() 为椭圆的左顶点,是否存在不同于点
为椭圆的左顶点,是否存在不同于点![]() 的定点
的定点![]() ,对于圆
,对于圆![]() 上任意一点
上任意一点![]() ,都有
,都有![]() 为常数,若存在,求所有满足条件的点
为常数,若存在,求所有满足条件的点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
解:(1)设椭圆的方程为![]() ,由题意可得:
,由题意可得:
椭圆C两焦点坐标分别为![]() ,
,![]()
由点![]() 在该椭圆上,
在该椭圆上,![]() .
.
![]() 又
又![]() 得
得 ![]() ,--3分, 故椭圆的方程为
,--3分, 故椭圆的方程为![]() .
.
(2)设点P的坐标为![]() ,则
,则![]() -----------①
-----------①
由![]() 得
得![]() ,∴
,∴![]() ,即
,即![]() -②
-②
由①②联立结合![]() 解得:
解得: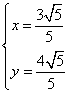 ,即点P的坐标为
,即点P的坐标为![]()
∴直线![]() 的方程为
的方程为![]()
∵圆![]() 的圆心O到直线
的圆心O到直线![]() 的距离
的距离![]() ∴直线
∴直线![]() 与⊙O相切
与⊙O相切
(3)的坐标为![]() ,则
,则![]() ,假设存在点
,假设存在点![]() ,对于
,对于![]() 上任意一点
上任意一点![]() ,都有
,都有![]() 为常数,则
为常数,则![]() ,
,![]()
∴![]() (常数)恒成立
(常数)恒成立
又x2+y2=4, 可得:![]() 恒成立
恒成立
∴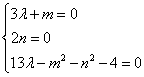 ∴
∴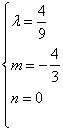 或
或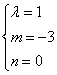 (不合舍去)
(不合舍去)
∴存在满足条件的点B,它的坐标为![]()

练习册系列答案
相关题目
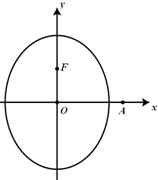 (2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=
(2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=
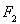
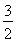
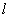

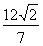
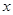 轴上,离心率为
轴上,离心率为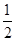 ,且点
,且点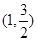 在该椭圆上。
在该椭圆上。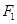 的直线
的直线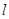 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若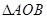 的面积为
的面积为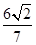 ,求圆心在原点O且与直线相切的圆的方程。
,求圆心在原点O且与直线相切的圆的方程。