题目内容
【题目】关于不同的直线![]() 与不同的平面
与不同的平面![]() ,有下列六个命题:
,有下列六个命题:
①若![]() 则
则![]() ;
;
②若![]() 则
则![]() ;
;
③若![]() 且
且![]() 则
则![]() ;
;
④若![]() 且
且![]() 则
则![]() ;
;
⑤若![]() 且
且![]() 则
则![]() ;
;
⑥若![]() 且
且![]() 则
则![]() ;
;
其中正确命题的序号是__________;
【答案】①③⑤
【解析】
①:根据线面平行的性质定理、面面垂直的判定定理,结合平行线的性质进行判断即可;
②:根据线面平行的判定定理进行判断即可;
③:根据线面平行的性质定理、面面平行的性质,以及平行线的性质进行判断即可;
④:在正方体中可以找到特例进行判断即可;
⑤:根据平面法向量的性质和空间向量夹角公式进行判断即可;
⑥:根据面面平行的性质,结合直线与直线的位置关系进行判断即可.
①:因为![]() ,所以存在过直线
,所以存在过直线![]() 的一个平面与平面
的一个平面与平面![]() 交于直线
交于直线![]() ,显然有
,显然有![]() ,而
,而![]() ,所以
,所以![]() ,而
,而![]() ,因此
,因此![]() ,故本命题是真命题;
,故本命题是真命题;
②:只有当![]() ,
,![]() 才能推出
才能推出![]() ,故本命题是假命题;
,故本命题是假命题;
③:因为![]() ,所以存在过直线
,所以存在过直线![]() 的一个平面与平面
的一个平面与平面![]() 交于直线
交于直线![]() ,显然有
,显然有![]() ,又
,又![]() ,所以
,所以![]() ,因此
,因此![]() ,所以
,所以![]() ,故本命题是真命题;
,故本命题是真命题;
④:在如图的正方体![]() 中:
中:
平面![]() 记为平面
记为平面![]() ,平面
,平面![]() 记为平面
记为平面![]() ,直线
,直线![]() 记为直线
记为直线![]() ,直线
,直线![]() 记为直线
记为直线![]() ,显然符合
,显然符合![]()
![]() ,但是
,但是![]() ,(当然
,(当然![]() 也可以是异面直线),故本命题是假命题,
也可以是异面直线),故本命题是假命题,

⑤:因为![]() ,所以平面
,所以平面![]() 的法向量分别为:
的法向量分别为:![]() ,因为
,因为![]() 所以为
所以为![]() ,故本命题是真命题;
,故本命题是真命题;
⑥:因为![]() 且
且![]() 所以直线
所以直线![]() 没有交点,故两直线是平行线或异面直线,故本命题是假命题.
没有交点,故两直线是平行线或异面直线,故本命题是假命题.
故答案为:①③⑤

【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查,对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如下表所示:
中学编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
卫生标准评分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;(精确到0.1)
(2)现从8个被检查的中学食堂中任意抽取两个组成一组,若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分,则组成“对比标兵食堂”,求该组被评为“对比标兵食堂”的概率.
参考公式: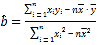 ,
,![]() ;
;
参考数据:![]() ,
,![]() .
.


