��Ŀ����
1����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0����������Ϊ$\frac{\sqrt{2}}{2}$�����ҽ���ֱ�ΪF1��F2��F1������x���غϵ�ֱ��l1������ԲC����P��Q���㣬����PQF2���ܳ�Ϊ4$\sqrt{2}$����1������ԲC�ı�����
��2����F1����ֱ��l1��ֱ��ֱ��l2����l2����ԲC���ڵ�M��N���㣬���ı���PMQN�����ȡֵ��Χ��
���� ��1������Բ�Ķ���ɵ�4a=4$\sqrt{2}$���������ʹ�ʽ��a��b��c�Ĺ�ϵ���ⷽ�̿ɵ�a��b�������õ���Բ���̣�
��2������ֱ��l1��б�ʲ����ںʹ��ڣ����ֱ�߷��̣�������Բ���̣���Τ�ﶨ�����ҳ���ʽ���Լ��ı��ε������ʽ���������������ɻ�������ʽ���ɵõ�����Χ��
��� �⣺��1������Բ�Ķ���ɵ�4a=4$\sqrt{2}$����e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$����a2=b2+c2��
�ⷽ�̿ɵ�a=$\sqrt{2}$��b=1��c=1��
����������ԲC����Բ����Ϊ$\frac{{x}^{2}}{2}$+y2=1��
��2����ֱ��l1б�ʲ����ڣ����ʱ|PQ|=$\sqrt{2}$��|MN|=2$\sqrt{2}$��
�ı���PQMN�����S=$\frac{1}{2}$|PQ|•|MN|=2��
��ֱ��l1��б�ʴ����Ҳ�Ϊ0�������l1��y=k��x+1����P��x1��y1����Q��x2��y2����
������Բ���̣���ȥy�ã���1+2k2��x2+4k2x+2k2-2=0��
|PQ|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\frac{\sqrt{��4{k}^{2}��^{2}-4��2{k}^{2}-2����2{k}^{2}+1��}}{1+2{k}^{2}}$•$\sqrt{1+{k}^{2}}$=2$\sqrt{2}$•$\frac{1+{k}^{2}}{1+2{k}^{2}}$��
ͬ������-$\frac{1}{k}$ ����k����|MN|=2$\sqrt{2}$•$\frac{1+{k}^{2}}{2+{k}^{2}}$��
���ı���PQMN�����S=$\frac{1}{2}$|PQ|•|MN|=4•$\frac{1+2{k}^{2}+{k}^{4}}{2+5{k}^{2}+2{k}^{4}}$=4��$\frac{1}{2}$-$\frac{{k}^{2}}{4{k}^{4}+10{k}^{2}+4}$��
=4��$\frac{1}{2}$-$\frac{1}{4{k}^{2}+\frac{4}{{k}^{2}}+10}$������4k2+$\frac{4}{{k}^{2}}$��2$\sqrt{4{k}^{2}•\frac{4}{{k}^{2}}}$=8�����ҽ���k2=1ʱ�Ⱥų�����
����$\frac{1}{4{k}^{2}+\frac{4}{{k}^{2}}+10}$�ʣ�0��$\frac{1}{16}$]���� 4��$\frac{1}{2}$-$\frac{1}{4{k}^{2}+\frac{4}{{k}^{2}}+10}$����[$\frac{16}{9}$��2����
�����������ı���PQMN�����S��[$\frac{16}{9}$��2]��
���� ���⿼����Բ�ķ��̵�������ֱ�ߺ���Բ��������������Τ�ﶨ�����ҳ���ʽ�������ı�������ķ�Χ����ע�����û�������ʽ���������������������е��⣮

 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�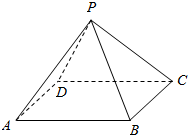 ��ͼ��P-ABCD��һ�����ⳤ��Ϊ2cm������������������ı�����������
��ͼ��P-ABCD��һ�����ⳤ��Ϊ2cm������������������ı�����������