题目内容
已知:四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点,PA=a,∠PDA=45º(1)求证:AF∥平面PCE;(2)求证:平面PCE⊥平面PCD;(3)求点D到平面PCE的距离.

(1)证明:取PC的中点为G,连结FG、EG
![]() ∵FG∥DC FG=
∵FG∥DC FG=![]() DC DC∥AB AE=
DC DC∥AB AE=![]() AB
AB
∴FG∥AE
∴四边形AFGE为平行四边形
∴AF∥EG 又∵AF![]() 平面PCE EG
平面PCE EG![]() 平面PCE
平面PCE
∴AF∥平面PCE
(2)证明:∵PA⊥平面ABCD AD⊥DC ∴PD⊥DC
∴∠PDA为二面角P-CD-B的平面角 ∴∠PDA=45º,即△PAD为等腰直角三角形
又∵F为PD的中点 AF⊥PD ①
由DC⊥AD DC⊥PD AD∩PD=D
得:DC⊥平面PAD 而AF![]() 平面PAD
平面PAD
∴ AF⊥DC ②
由①②得AF⊥平面PDC 而EG∥AF
∴EG⊥平面PDC 又EG![]() 平面PCE
平面PCE
∴平面PCE⊥平面PDC
(3)解:过点D作DH⊥PC于H
∵平面PCE⊥平面PDC ∴DH⊥平面PEC
即DH的长为点D到平面PEC的距离
在Rt△PAD中,PA=AD=a PD=![]() a
a
在Rt△PDC中,PD=![]() a,CD=a
a,CD=a
PC=![]() a DH=
a DH=![]() a
a
即:点D到平面PCE的距离为![]() a。
a。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
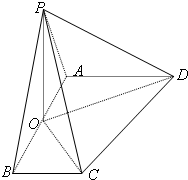 已知在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,O为AB中点,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3.
已知在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,O为AB中点,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3. (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.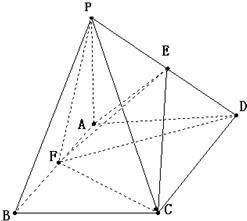 已知:四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,且PA=AB=2,PC与底面ABCD所成角为450,PD的中点为E,F为AB上的动点.
已知:四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,且PA=AB=2,PC与底面ABCD所成角为450,PD的中点为E,F为AB上的动点. (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.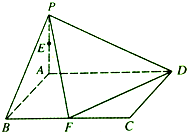 已知在四棱锥P-ABCD,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段PA,BC的中点.
已知在四棱锥P-ABCD,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段PA,BC的中点.