题目内容
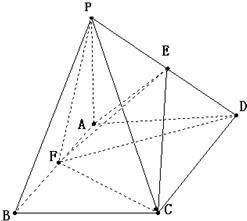 已知:四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,且PA=AB=2,PC与底面ABCD所成角为450,PD的中点为E,F为AB上的动点.
已知:四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,且PA=AB=2,PC与底面ABCD所成角为450,PD的中点为E,F为AB上的动点.(1)求三棱锥E-FCD的体积;
(2)当点F为AB中点时,试判断AE与平面PCF的位置关系,并说明理由.
分析:(1)根据直线与平面所成角的定义,先在Rt△PAC中计算出PA=AC=2,从而得到底面菱形ABCD的对角线AC与边长相等,得到底面的面积为
.再根据F在菱形ABCD的一条边上,可得△FCD面积等于菱形ABCD面积的一半,又因为PD的中点为E,所以E到平面FCD的距离等于P到平面FCD的距离即PA的一半,从而得到三棱锥E-FCD的体积等于三棱锥P-FCD的体积的一半,不难算出这个体积;
(2)取PC中点G,连接FG、EG,利用三角形中位线定理可以证明出四边形AEGF是平行四边形,从而AE∥BG,最后用直线与平面平行的判定定理得出AE与平面PCF平行的位置关系.
| 3 |
(2)取PC中点G,连接FG、EG,利用三角形中位线定理可以证明出四边形AEGF是平行四边形,从而AE∥BG,最后用直线与平面平行的判定定理得出AE与平面PCF平行的位置关系.
解答: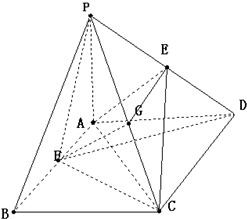 解:(1)连AC,因为PA⊥平面ABCD,
解:(1)连AC,因为PA⊥平面ABCD,
∴∠PCA为PC与底面ABCD所成角,
即∠PCA=45°,∴PA=AC=2,AC=AB=BC=2,
∴S△FCD=
×2×
=
.
因为E为PD的中点,
∴VE-FCD=
VP-FCD
=
•
S△FCD•PA
=
•
•2
=
…(6分)
(2)当点F为AB中点时,AE∥平面PCF…(7分)
下面证明这一结论:
设PC的中点为G,连接FG,EG,
则EG∥CD,且EG=
CD.
又∵四边形ABCD是菱形,点F为AB中点,
∴EG∥AF,且EG=AF,
∴四边形AEGF为平行四边形,
∴AE∥GF.
又∵GF?平面PFC,AE?平面PFC,
∴AE∥平面PFC…(12分)
 解:(1)连AC,因为PA⊥平面ABCD,
解:(1)连AC,因为PA⊥平面ABCD,∴∠PCA为PC与底面ABCD所成角,
即∠PCA=45°,∴PA=AC=2,AC=AB=BC=2,
∴S△FCD=
| 1 |
| 2 |
| 3 |
| 3 |
因为E为PD的中点,
∴VE-FCD=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 3 |
=
| 1 |
| 6 |
| 3 |
=
| ||
| 3 |
(2)当点F为AB中点时,AE∥平面PCF…(7分)
下面证明这一结论:
设PC的中点为G,连接FG,EG,
则EG∥CD,且EG=
| 1 |
| 2 |
又∵四边形ABCD是菱形,点F为AB中点,
∴EG∥AF,且EG=AF,
∴四边形AEGF为平行四边形,
∴AE∥GF.
又∵GF?平面PFC,AE?平面PFC,
∴AE∥平面PFC…(12分)
点评:本题综合了直线与平面平行的判定、直线与平面垂直的性质和棱柱、棱锥、棱台的体积等几个知识点,考查了同学们对空间位置关系的认识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
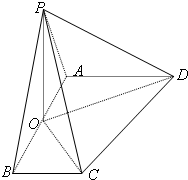 已知在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,O为AB中点,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3.
已知在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,O为AB中点,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3. (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点. (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.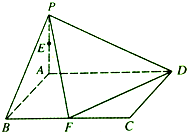 已知在四棱锥P-ABCD,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段PA,BC的中点.
已知在四棱锥P-ABCD,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段PA,BC的中点.