题目内容
试用函数单调性的定义判断函数f(x)=| 2x | x-1 |
分析:本题考查的是函数的单调性证明问题.在解答时,首先要结合定义域和所给区间任设两个变量并保证大小关系,然后通过作差法即可获得相应变量对应函数值的大小关系,结合函数单调性的定义即可获得问题的解答.
解答:证明:任取x1,x2∈(0,1),且x1<x2,
则f(x1)-f(x2)=
-
═
由于0<x1<x2<1,x1-1<0,x2-1<0,x2-x1>0,
故f(x1)-f(x2)>0,
即f(x1)>f(x2).
所以函数f(x)=
在(0,1)上是减函数.
则f(x1)-f(x2)=
| 2x1 |
| x1-1 |
| 2x2 |
| x2-1 |
| 2(x2-x1) |
| (x1-1)(x2-1) |
由于0<x1<x2<1,x1-1<0,x2-1<0,x2-x1>0,
故f(x1)-f(x2)>0,
即f(x1)>f(x2).
所以函数f(x)=
| 2x |
| x-1 |
点评:本题考查的是函数的单调性证明问题.在解答的过程当中充分体现了函数单调性的定义、作差法以及分解因式等知识.值得同学们体会和反思.

练习册系列答案
相关题目
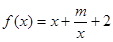 (
(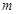 为实常数).
为实常数).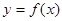 图像上动点
图像上动点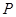 到定点
到定点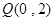 的距离的最小值为
的距离的最小值为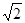 ,求实数
,求实数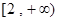 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数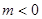 ,若不等式
,若不等式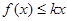 在
在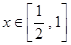 有解,求
有解,求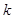 的取值范围.
的取值范围. 有如下性质:如果常数
有如下性质:如果常数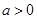 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值;
的值;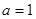 时,试用函数单调性的定义证明函数f(x)在
时,试用函数单调性的定义证明函数f(x)在 上是减函数。
上是减函数。 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值;