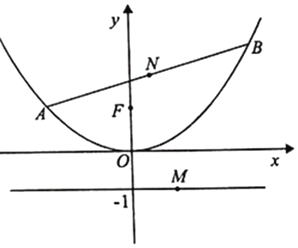
题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,若过
,若过![]() 且倾斜角为
且倾斜角为![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,满足
两点,满足![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() 为
为![]() 上动点,
上动点,![]() ,
,![]() 在
在![]() 轴上,圆
轴上,圆![]() 内切于
内切于![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求出抛物线的焦点,设出直线![]() 的方程,代入抛物线方程,运用韦达定理和抛物线的定义,可得
的方程,代入抛物线方程,运用韦达定理和抛物线的定义,可得![]() ,进而得到抛物线方程;(2)设
,进而得到抛物线方程;(2)设![]() ,
,![]() ,
,![]() ,不妨设
,不妨设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,由直线与圆相切的条件:
,由直线与圆相切的条件:![]() ,化简整理,结合韦达定理以及三角形的面积公式,运用基本不等式即可求得最小值.
,化简整理,结合韦达定理以及三角形的面积公式,运用基本不等式即可求得最小值.
(1)抛物线![]() 的焦点为
的焦点为![]() ,
,
则过点![]() 且斜率为1的直线方程为
且斜率为1的直线方程为![]() ,
,
联立抛物线方程![]() ,
,
消去![]() 得:
得:![]() ,
,
设![]() ,则
,则![]() ,
,
由抛物线的定义可得![]() ,解得
,解得![]() ,
,
所以抛物线的方程为![]()
(2)设![]() ,
,![]() ,
,![]() ,
,
不妨设![]() ,
,![]()
化简得:![]() ,
,
圆心![]() 到直线
到直线![]() 的距离为1,
的距离为1,
故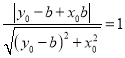 ,
,
即![]() ,不难发现
,不难发现![]() ,
,
上式又可化为![]() ,
,
同理有![]() ,
,
所以![]() 可以看做关于
可以看做关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根,
的两个实数根,
![]() ,
,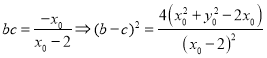 ,
,
由条件:![]()
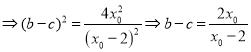
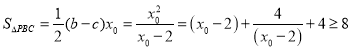 ,
,
当且仅当![]() 时取等号.
时取等号.
∴![]() 面积的最小值为8.
面积的最小值为8.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
【题目】有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
| 明文字符 | A | B | C | D |
密码字符 | 11 | 12 | 13 | 14 | |
| 明文字符 | E | F | G | H |
密码字符 | 21 | 22 | 23 | 24 | |
| 明文字符 | M | N | P | Q |
密码字符 | 1 | 2 | 3 | 4 |
设随机变量![]() 表示密码中不同数字的个数.
表示密码中不同数字的个数.
(Ⅰ)求![]() 的分布列和它的数学期望.
的分布列和它的数学期望.