题目内容
如图,为了计算衡水湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,求两景点B与C之间的距离(假设A,B,C,D在同一平面内,测量结果保留整数;参考数据:![]() =1.414,
=1.414,![]() =1.732,
=1.732,![]() =2.236).
=2.236).

解:在△ABD中,设BD=xm,
则BA2=BD2+AD2-2BD·AD·cos∠BDA,
即1402=x2+1002-2×100×x×cos60°,
整理得x2-100x-9600=0,
解之得x1=160,x2=-60(舍去),
故BD=160m,
由正弦定理,得:![]() =
=![]() ,
,
又AD⊥CD,∴∠CDB=30°,
∴BC=![]() ·sin30°=80
·sin30°=80![]() ≈113(m).
≈113(m).
即两景点B与C之间的距离约为113m.

练习册系列答案
相关题目
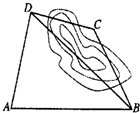 如图,为了计算郑东新区龙湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=5km,AB=7km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离.(假设A,B,C,D在同一平面内)
如图,为了计算郑东新区龙湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=5km,AB=7km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离.(假设A,B,C,D在同一平面内)
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两个测量点,现测得
两个测量点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点 在同一平面内,测量结果保留整数;参考数据:
在同一平面内,测量结果保留整数;参考数据: )
)
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两个测量点,现测得
两个测量点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点 在同一平面内,测量结果保留整数;参考数据:
在同一平面内,测量结果保留整数;参考数据: )
)