题目内容
有人玩掷正四面体骰子走跳棋的游戏,已知正四面体骰子四个面上分别印有A,B,C,D,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为A面,棋子向前跳2站,若掷出后骰子为B,C,D中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn(n∈N).(Ⅰ)求P0,P1,P2;
(Ⅱ)求证:Pn-Pn-1=-
| 1 | 4 |
(Ⅲ)求玩该游戏获胜的概率.
分析:(Ⅰ)理解P0,P1,P2的含义分别计算即可;
(Ⅱ)棋子跳到第n站(2≤n≤99)有两种可能:第一种,棋子先到第n-2站,又掷出后得到A面,第二种,棋子先到第 n-1站,又掷出后得到B,C,D 中的一面,
(Ⅲ)利用(Ⅱ)的结论,转化为等比数列,再用累加法求解
(Ⅱ)棋子跳到第n站(2≤n≤99)有两种可能:第一种,棋子先到第n-2站,又掷出后得到A面,第二种,棋子先到第 n-1站,又掷出后得到B,C,D 中的一面,
(Ⅲ)利用(Ⅱ)的结论,转化为等比数列,再用累加法求解
解答:解:(1)依题意,得P0=1,P1=
,P2=
(Ⅱ)设棋子跳到第n站(2≤n≤99)有两种可能:第一种,棋子先到第n-2站,又掷出后得到A面,其概率为
Pn-2;第二种,棋子先到第 n-1站,又掷出后得到B,C,D 中的一面,其概率为
Pn-1,由于以上两种可能是互斥的,所以Pn=
Pn-1+
Pn-2,即有Pn-Pn-1=-
(Pn-1-Pn-2)
(Ⅲ)由(Ⅱ)知数列 {Pn-Pn-1}是首项为P1-P0=-
,公比为 -
的等比数列.
于是有P1-P0=-
,P99-P98=(-
)99.
把以上各式相加,得.P99=
[1-(-
)100]
因此,获胜的概率为
[1-(-
)100]
| 3 |
| 4 |
| 13 |
| 16 |
(Ⅱ)设棋子跳到第n站(2≤n≤99)有两种可能:第一种,棋子先到第n-2站,又掷出后得到A面,其概率为
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(Ⅲ)由(Ⅱ)知数列 {Pn-Pn-1}是首项为P1-P0=-
| 1 |
| 4 |
| 1 |
| 4 |
于是有P1-P0=-
| 1 |
| 4 |
| 1 |
| 4 |
把以上各式相加,得.P99=
| 4 |
| 5 |
| 1 |
| 4 |
因此,获胜的概率为
| 4 |
| 5 |
| 1 |
| 4 |
点评:将概率与数列联系起来,关键是合理地将问题等价转化,构造新数列,从而利用等比数列的求和公式进行求解.

练习册系列答案
相关题目
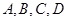 ,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为
,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为 面,棋子向前跳2站,若掷出后骰子为
面,棋子向前跳2站,若掷出后骰子为 中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为
中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为 (
(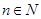 ).
).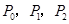 ;
; ;
; ;
;