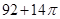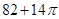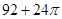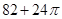题目内容
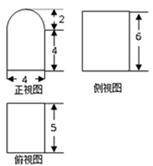
一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的体积为( )
| A．1 |
B． |
C． |
D． |
B
解析由三视图可知，此几何体为三棱锥，如图，
其中正视图为
，是边长为2的正三角形，
，且
，底面
为等腰直角三角形，
，所以体积为
，故选B.
练习册系列答案
相关题目
某四棱锥的三视图如图所示，则最长的一条侧棱长度为（ ）
A． | B． |
C． | D． |
正四面体的外接球和内切球的半径的关系是( )
A． |
B． |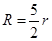
C． |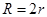
D． |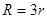
棱长为2的三棱锥的外接球的表面积为（ ）
| A．6π | B．4π | C．2π | D．π |
某三棱锥的三视图如图所示，该三棱锥的表面积是（ ）
A．28+6 | B．30+6 | C．56+12 | D．60+12 |
若两个球的表面积之比为1：4，则这两个球的体积之比为（ ）
| A．1：2 | B．1：4 | C．1：8 | D．1：16 |
