题目内容
正四面体的外接球和内切球的半径的关系是( )
A. |
B.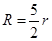 |
C.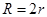 |
D.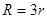 |
D
解析如图所示,设点 是内切球的球心,正四面体棱长为
是内切球的球心,正四面体棱长为 .由图形的对称性知,点
.由图形的对称性知,点 也是外接球的球心.设内切球半径为
也是外接球的球心.设内切球半径为 ,外接球半径为
,外接球半径为 .
.

在 中,
中, ,即
,即 ,得
,得 ,得
,得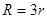 ,故选D.
,故选D.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( )
| A.1 |
B. |
C. |
D. |
已知三棱柱
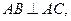

A.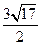 |
B. |
C. |
D.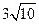 |
四面体 中,
中, 与
与 互相垂直,
互相垂直,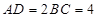 ,且
,且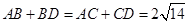 ,则四面体
,则四面体 的体积的最大值是( ) .
的体积的最大值是( ) .
| A.4 | B.2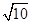 | C.5 | D. |
 、
、 是半径为
是半径为 的球
的球 的球面上两点,它们的球面距离为
的球面上两点,它们的球面距离为 ,求过
,求过 、
、 的平面中,与球心的最大距离是( )
的平面中,与球心的最大距离是( )
A. |
B. |
C. |
D. |
四面体 中,
中, 则四面体外接球的表面积为( )
则四面体外接球的表面积为( )
A. |
B. |
C. |
D. |








