题目内容
已已知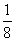 请根据上述两个等式计算cos(α-β)与cos(α+β)的值.
请根据上述两个等式计算cos(α-β)与cos(α+β)的值.
解:将已知两式平方后相加,得
2+2(sinαsinβ+cosαcosβ)=![]() +
+![]() ,
,
cosαcosβ+sinαsinβ=-![]() ,
,
∴cos(α-β)=-![]() .
.
将已知两式平方后相减,结合cos(α-β)=-![]() ,
,
得![]() =cos2α-sin2α+cos2β-sin2β+2(cosαcosβ-sinαsinβ)=cos2α+cos2β+2cos(α+β)
=cos2α-sin2α+cos2β-sin2β+2(cosαcosβ-sinαsinβ)=cos2α+cos2β+2cos(α+β)
=cos[(α+β)+(α-β)]+cos[(α+β)-(α-β)]+2cos(α+β)
=2cos(α+β)·cos(α-β)+2cos(α+β)
=![]() cos(α+β),∴cos(α+β)=
cos(α+β),∴cos(α+β)=![]() .
.

练习册系列答案
相关题目
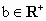 ,且a+b=1,那么
,且a+b=1,那么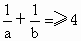 .
.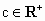 ,且a+b+c=1,推广上述已知命题,能得到什么不等式?请加以证明;
,且a+b+c=1,推广上述已知命题,能得到什么不等式?请加以证明; ,且
,且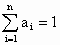 ,推广上述已知命题,能得到什么不等式?请加以证明.
,推广上述已知命题,能得到什么不等式?请加以证明.