题目内容
在数列{an}中，已知
，
，当n≥2且n∈N*时，有
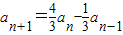．（1）若bn=an+1-an（n∈N*），求证：数列{bn}是等比数列；
（2）求证：对任意n∈N*，都有
．
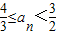【答案】分析：（1）根据题意在数列{an}中，已知
，
，根据等比数列的性质，证明
等于一个常数即可；
（2）数列{bn}是等比数列，
，可得对an进行拆分，可得an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1，然后进行求和，再进行证明；
解答：解：（1）当n=1时，有
…（1分）
当n≥2时，有
=
故数列{bn}是等比数列，其首项为
，公比为
…（5分）
（2）由（1）知
即
…（6分）
故an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1=
…（10分）
当n∈N*时，有
，故
，
故
，即
…（13分）
点评：此题主要考查等比数列的性质，是一道中档题，第二问对an进行拆分求和，考查的知识点比较全面；
，，根据等比数列的性质，证明等于一个常数即可；（2）数列{bn}是等比数列，
，可得对an进行拆分，可得an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1，然后进行求和，再进行证明；解答：解：（1）当n=1时，有
…（1分）当n≥2时，有
=故数列{bn}是等比数列，其首项为
，公比为…（5分）（2）由（1）知
即…（6分）故an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1=
…（10分）当n∈N*时，有
，故，故
，即…（13分）点评：此题主要考查等比数列的性质，是一道中档题，第二问对an进行拆分求和，考查的知识点比较全面；
练习册系列答案
相关题目