题目内容
已知数列{an}、{bn},an>0,a1=6,点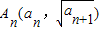 在抛物线y2=x+1上;点Bn(n,bn)在直线y=2x+1上.
在抛物线y2=x+1上;点Bn(n,bn)在直线y=2x+1上.(1)求数列{an}、{bn}的通项公式;
(2)若
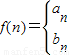
 ,问是否存在k∈N*,使f(k+15)=2f(k)成立,若存在,求出k值;若不存在,说明理由;
,问是否存在k∈N*,使f(k+15)=2f(k)成立,若存在,求出k值;若不存在,说明理由;(3)对任意正整数n,不等式
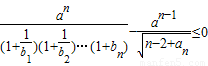 成立,求正实数a的取值范围.
成立,求正实数a的取值范围.
【答案】分析:(1)由点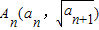 在抛物线y2=x+1上,知an+1=an+1,由此能求出an=n+5.由点Bn(n,bn)在直线y=2x+1上.能求出bn=2n+1.
在抛物线y2=x+1上,知an+1=an+1,由此能求出an=n+5.由点Bn(n,bn)在直线y=2x+1上.能求出bn=2n+1.
(2)由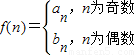 ,知当k为奇数时,k+15为偶数,故2(k+15)+1=2(k+5),显然不成立.当k为偶数时,k+15为奇数,则有k+20=2(2k+1),由此能求出k.
,知当k为奇数时,k+15为偶数,故2(k+15)+1=2(k+5),显然不成立.当k为偶数时,k+15为奇数,则有k+20=2(2k+1),由此能求出k.
(3)由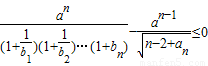 ,得:
,得: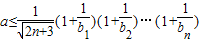 ,记g(n)=
,记g(n)=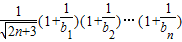 ,由此能求出正实数a的取值范围.
,由此能求出正实数a的取值范围.
解答:解:(1)∵点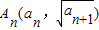 在抛物线y2=x+1上,
在抛物线y2=x+1上,
∴an+1=an+1,
∵an>0,a1=6,
∴{an}是首项a1=6,公差d=an+1-an=1的等差数列,
∴an=n+5.
∵点Bn(n,bn)在直线y=2x+1上.
∴bn=2n+1…(4分)
(2)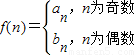 ,
,
当k为奇数时,k+15为偶数,
∴2(k+15)+1=2(k+5),显然不成立.
当k为偶数时,k+15为奇数,则有k+20=2(2k+1),解得k=6.…(8分)
(3)由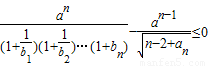 ,
,
得: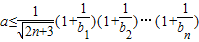 ,
,
记g(n)=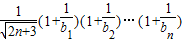 ,
,
则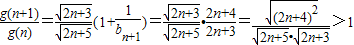
∴g(n+1)>g(n),即g(n)递增.
∴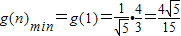 ,
,
即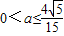 .…(13分)
.…(13分)
点评:本题考查数列的通项公式的求法、实数k是否存在的判断和求正实数a的取值范围.综合性强,难度大,是高考的重点.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
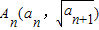 在抛物线y2=x+1上,知an+1=an+1,由此能求出an=n+5.由点Bn(n,bn)在直线y=2x+1上.能求出bn=2n+1.
在抛物线y2=x+1上,知an+1=an+1,由此能求出an=n+5.由点Bn(n,bn)在直线y=2x+1上.能求出bn=2n+1.(2)由
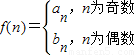 ,知当k为奇数时,k+15为偶数,故2(k+15)+1=2(k+5),显然不成立.当k为偶数时,k+15为奇数,则有k+20=2(2k+1),由此能求出k.
,知当k为奇数时,k+15为偶数,故2(k+15)+1=2(k+5),显然不成立.当k为偶数时,k+15为奇数,则有k+20=2(2k+1),由此能求出k.(3)由
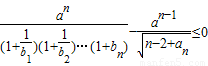 ,得:
,得: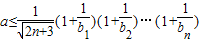 ,记g(n)=
,记g(n)=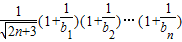 ,由此能求出正实数a的取值范围.
,由此能求出正实数a的取值范围.解答:解:(1)∵点
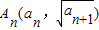 在抛物线y2=x+1上,
在抛物线y2=x+1上,∴an+1=an+1,
∵an>0,a1=6,
∴{an}是首项a1=6,公差d=an+1-an=1的等差数列,
∴an=n+5.
∵点Bn(n,bn)在直线y=2x+1上.
∴bn=2n+1…(4分)
(2)
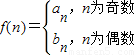 ,
,当k为奇数时,k+15为偶数,
∴2(k+15)+1=2(k+5),显然不成立.
当k为偶数时,k+15为奇数,则有k+20=2(2k+1),解得k=6.…(8分)
(3)由
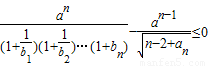 ,
,得:
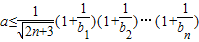 ,
,记g(n)=
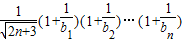 ,
,则
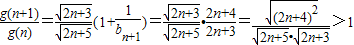
∴g(n+1)>g(n),即g(n)递增.
∴
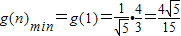 ,
,即
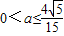 .…(13分)
.…(13分)点评:本题考查数列的通项公式的求法、实数k是否存在的判断和求正实数a的取值范围.综合性强,难度大,是高考的重点.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目