题目内容
函数
- A.在（-∞，e）上单调递增
- B.在（-∞，0）和（0，e）上单调递增
- C.在（e，+∞）上单调递增
- D.在（0，e）上单调递增
D
分析：由已知中函数的解析式，我们易求出函数的导函数的解析式，进而求出f′（x）＞0成立的区间及f′（x）＜0成立的区间，即可得到函数的单调性，进而得到答案．
解答：∵函数
∴
∵当x∈（0，e）时，f′（x）＞0恒成立，故函数在（0，e）上单调递增
当x∈（e，+∞）时，f′（x）＜0恒成立，故函数在（e，+∞）上单调递减
故选D
点评：本题考查的知识点是利用导数研究函数的单调性，其中根据函数的解析式得到导函数的解析式，进而判断导函数在各区间上的符号是解答本题的关键．
分析：由已知中函数的解析式，我们易求出函数的导函数的解析式，进而求出f′（x）＞0成立的区间及f′（x）＜0成立的区间，即可得到函数的单调性，进而得到答案．
解答：∵函数
∴
∵当x∈（0，e）时，f′（x）＞0恒成立，故函数
在（0，e）上单调递增当x∈（e，+∞）时，f′（x）＜0恒成立，故函数
在（e，+∞）上单调递减故选D
点评：本题考查的知识点是利用导数研究函数的单调性，其中根据函数的解析式得到导函数的解析式，进而判断导函数在各区间上的符号是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
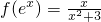，x∈R．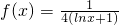
有两个不相等的实数根α，β，求αβ的值；
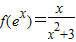，x∈R．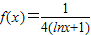
有两个不相等的实数根α，β，求αβ的值；