题目内容
如图,在正方体ABCD—A1B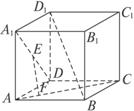
证明:连结A
∴EF⊥A
又EF⊥A1D,A1D∩A
∴EF⊥平面A
∵BB1⊥平面A1B
平面A1B
∴BB1⊥A
∵四边形A1B
∴A
∴A
而BD1
平面BB1D1D,
∴A
同理,DC1⊥BD1,DC1∩A
∴BD1⊥平面A
由①②可知EF∥BD1.
小结:证明EF∥BD1,构造与EF、BD1都垂直的平面是关键.由于EF是AC和A1D的公垂线,这一条件对构造线面垂直十分有用.
练习册系列答案
相关题目
题目内容
如图,在正方体ABCD—A1B
证明:连结A
∴EF⊥A
又EF⊥A1D,A1D∩A
∴EF⊥平面A
∵BB1⊥平面A1B平面A1B
∴BB1⊥A
∵四边形A1B
∴A
∴A
而BD1平面BB1D1D,
∴A
同理,DC1⊥BD1,DC1∩A
∴BD1⊥平面A
由①②可知EF∥BD1.
小结:证明EF∥BD1,构造与EF、BD1都垂直的平面是关键.由于EF是AC和A1D的公垂线,这一条件对构造线面垂直十分有用.
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体ABCD-A1B1C1D1中，E为DD1的中点，
如图，在正方体ABCD-A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的主视图与左视图的面积的比值为（ ）