Question

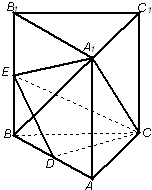如图，在直三棱柱ABC-A₁B₁C₁中，AC=BC=4，∠ACB=90°，AB=AA₁，点D是AB的中点，点E是BB₁的中点．
（1）求证：A₁B⊥平面CDE；
（2）求二面角D-CE-A₁的大小．

Answer 1

分析：（1）要证A₁B⊥平面CDE，只需证明A₁B⊥平面CDE中的两条相交直线，易证A₁B⊥AB₁，A₁B⊥DE，从而问题得证；
（2）先确定二面角D-CE-A₁的平面角．根据A₁B⊥平面CDE，设A₁B与DE交于点M，过M作MN⊥CE，垂足为N，连接A₁N，则A₁N⊥CE，则可知∠A₁NM即为二面角D-CE-A₁的平面角．从而可求

解答：解：（1）证明：在直三棱柱ABC-A₁B₁C₁中，
面A₁B⊥面ABC，又D为AB中点，∴CD⊥面A₁B，
∴CD⊥A₁B，∵AB=AA₁，∴A₁B⊥AB₁，
又DE∥AB₁∴A₁B⊥DE，又DE∩CD=D
∴A₁B⊥平面CDE
（2）由（Ⅰ）知A₁B⊥平面CDE，设A₁B与DE交于点M，过M作MN⊥CE，垂足为N，连接A₁N，则A₁N⊥CE，
故∠A₁NM即为二面角D-CE-A₁的平面角．
∵CE=

BC2+BE2

=

6

，EM=

1

4

AB1=1，
又由△ENM△EDC得MN=

CD•ME

CE

=

3

3

．  
又∵A1M=

3

4

A1B=3，∴BN=

BC•BE

CE

=

2 3

3

，BM=

1

4

A1B=

1

4

A A 2 1 +AB2

=

1

4

(2 2 )2+(2 2 )2

=1，
在Rt△A₁MN中，tan∠A₁NM=

A1M

MN

=3

3

，
故二面角D-CE-A₁的大小为arctan3

3

．

点评：本题以直三棱柱为载体，考查线面垂直，考查面面角，关键是正确利用线面垂直的判定定理．