题目内容
如图1,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 90°,
90°,![]() 是
是![]() 上的一个动点.现将该平行四边形沿对角线
上的一个动点.现将该平行四边形沿对角线![]() 折成直二面角
折成直二面角![]() ,如图2所示.
,如图2所示.
(1)若![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,且
的中点,且![]() ∥平面
∥平面![]() ,求证:
,求证:![]() ∥平面
∥平面![]() ;
;
(2)当图1中![]() +
+![]() 最小时,求图2中二面角
最小时,求图2中二面角![]() 的大小.
的大小.
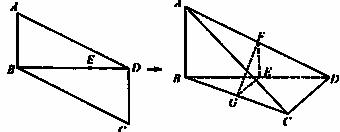
图1 图2
(1)证明: ∵![]() ∥平面
∥平面![]() ,平面
,平面![]() ∩平面
∩平面![]()
![]() ,∴
,∴![]() ∥
∥![]() .
.
∵![]() 是
是![]() 的中点.∴
的中点.∴![]() 是
是![]() 中点.
中点.
又∵![]() 是
是![]() 点.∴
点.∴![]() ∥
∥![]() .
.
∵![]()
![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.
(2)解:由图1可知,当![]() 最小时,
最小时,![]() 是
是![]() 的中点.
的中点.
∵平面![]() ⊥平面
⊥平面![]() ,
,![]() ⊥
⊥![]() ,
,![]() ⊥平面
⊥平面![]() .
.
故以![]() 为坐标原点,平行于
为坐标原点,平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() .
.

则![]() (0,0,1),
(0,0,1),![]() (1,
(1,![]() ,0),
,0),![]() (0,
(0,![]() ,0),
,0),![]() (0,
(0,![]() ,0);
,0);
![]()
![]() (0,--
(0,--![]() ,0),
,0),![]()
![]() (0,
(0,![]() ,0).
,0).
设平面![]() 的法向量为
的法向量为![]() =(
=(![]() ,
,![]() ,
,![]() ),则
),则

![]()

解得
∴平面![]() 的一个法向量为
的一个法向量为![]() =(-1,
=(-1,![]() ,1).
,1).
而平面![]() 的一个法向量为
的一个法向量为![]() =(0,0,1).
=(0,0,1).
∵![]() ,
,
显然,二面角![]() 为锐角,
为锐角,
∴二面角![]() 的大小为60°.
的大小为60°.

练习册系列答案
相关题目
 (2008•成都三模)如图1,在平行四边形ABCD中,AB=1,
(2008•成都三模)如图1,在平行四边形ABCD中,AB=1, ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.