题目内容
已知不等式
<0的解集为A,关于x的不等式(
)2x>2-a-x(a∈R)解集为B,全集U=R,求使∁UA∩B=B的实数a的取值范围.
| 2+x |
| x-1 |
| 1 |
| 2 |
考点:指、对数不等式的解法
专题:集合
分析:根据不等式的解法,求出对应的集合,即可得到结论.
解答:
解:由
<0解得-2<x<1,A=(-2,1).….(3分)
所以∁UA=(-∞,-2]∪[1,+∞).….(5分)
由(
)2x>2-a-x得(
)2x>(
)a+x,即2x<a+x,解得x<a.
所以B=(-∞,a).…(9分)
因为∁UA∩B=B,所以B⊆∁UA∩B,故有a≤-2.
即a的取值范围是(-∞,-2].…..(12分)
| 2+x |
| x-1 |
所以∁UA=(-∞,-2]∪[1,+∞).….(5分)
由(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以B=(-∞,a).…(9分)
因为∁UA∩B=B,所以B⊆∁UA∩B,故有a≤-2.
即a的取值范围是(-∞,-2].…..(12分)
点评:本题主要考查集合的基本运算,根据不等式的解法求出对应的集合是解决本题的关键.

练习册系列答案
相关题目
若数列{an}满足a1=1,a2=2,且an=
(n≥3),则a2010为( )
| an-1 |
| an-2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、22010 |
曲线y=
x3+
在点(2,4)处的切线方程是( )
| 1 |
| 3 |
| 4 |
| 3 |
| A、x+4y-4=0 |
| B、x-4y-4=0 |
| C、4x+y-4=0 |
| D、4x-y-4=0 |
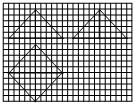 一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为
一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为