题目内容

（2012•芜湖二模）若|
a
|=1，|
b
|=2，
c
=
a
+
b
，且
c
⊥
a
，那么
a
与
b
的夹角为（　　）
分析：由向量垂直可得数量积为0，代入化简可得cosθ=-
1
2
，结合向量夹角的取值范围可得答案．
解答：解：∵
c
⊥
a
，∴
c
•
a
=0，，即(
a
+
b
).
a
=0，
a
2+
a
•
b
=0
设向量
a
，
b
的夹角为θ，
则有|
a
|2+|
a
|．|
b
|．cosθ=0，即1+2cosθ=0
解得cosθ=-
1
2
，又θ∈[0，π]，所以θ=120°
故选B
点评：本题考查向量夹角的求解，涉及数量积的运算及夹角公式，属基础题．
练习册系列答案
相关题目
（2012•芜湖二模）直线
x=1+
4
5
t
y=-1-
3
5
t
（t为参数）被曲线ρ=
2
cos(θ+
π
4
)所截的弦长为（　　）
（2012•芜湖二模）将一个四棱锥的每个顶点染上一种颜色，并使同一条棱上的两个端点异色，若只有5种颜色可供使用，则不同的染色方法总数有（　　）
（2012•芜湖二模）已知复数z=x+yi（x，y∈R），且有
x
1-i
=1+yi，
.
z
是z的共轭复数，那么
1
.
z
的值为（　　）
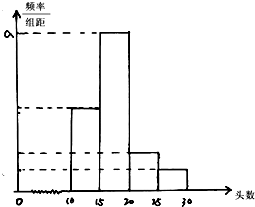（2012•芜湖二模）某省对省内养殖场“瘦肉精”使用情况进行检查，在全省的养殖场随机抽取M个养殖场的猪作为样本，得到M个养殖场“瘦肉精”检测阳性猪的头数，根据此数据作出了频率分布表和频率分布直方图如下：
分组 频数 频率
[10，15） 10 0.25
[15，20） 24 n
[20，25） m P
[25，30） 2 0.05
合计 M 1
（1）求出表中M，P以及图中a的值．
（2）若该省有这样规模的养殖场240个，试估计该省“瘦肉精”检测呈阳性的猪的头数在区间[10，15）内的养殖场的个数．
（3）在所取样本中，出现“瘦肉精”呈阳性猪的头数不少于20头的养殖场中任选2个，求至多一个养殖场出现“瘦肉精”阳性猪头数在区间[25，30）内的概率．
（2012•芜湖二模）抛物线y=8x2的焦点坐标为
(0，
1
32
)
(0，
1
32
)
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网