题目内容
曲线y=-x3+x2+2x与x轴所围成图形的面积为
- A.
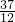
- B.3
- C.

- D.4
A
分析:先求得-x3+x2+2x=0的根,再利用定积分求出面积即可.
解答:由-x3+x2+2x=0,解得x=-1,0,2.
∴曲线y=-x3+x2+2x与x轴所围成图形的面积= +
+ =
= +
+ =
=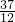 .
.
故选A.
点评:利用定积分求图形的面积是求图形面积的通法,一定要熟练掌握其解题步骤.
分析:先求得-x3+x2+2x=0的根,再利用定积分求出面积即可.
解答:由-x3+x2+2x=0,解得x=-1,0,2.
∴曲线y=-x3+x2+2x与x轴所围成图形的面积=
 +
+ =
= +
+ =
=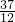 .
.故选A.
点评:利用定积分求图形的面积是求图形面积的通法,一定要熟练掌握其解题步骤.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目