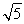题目内容
若双曲线与x2+4y2=64有相同的焦点,它的一条渐近线方程是x+
y=0,则双曲线的方程是( )
| 3 |
分析:依题意,可求得x2+4y2=64的焦点,也是双曲线的焦点,再由双曲线的一条渐近线方程即可求得双曲线的方程.
解答:解:∵x2+4y2=64?
+
=1,
∴该椭圆的焦点在x轴,且焦点坐标为:(±4
,0);
∵双曲线与x2+4y2=64有相同的焦点,
∴该双曲线的焦点在x轴,且焦点坐标为:(±4
,0),可排除B,C,D;
对于A,
-
=1,其焦点坐标为:(±4
,0),渐近线方程为y=±
x=±
x,其中之一即为x+
y=0,符合题意.
故选A.
| x2 |
| 64 |
| y2 |
| 16 |
∴该椭圆的焦点在x轴,且焦点坐标为:(±4
| 3 |
∵双曲线与x2+4y2=64有相同的焦点,
∴该双曲线的焦点在x轴,且焦点坐标为:(±4
| 3 |
对于A,
| x2 |
| 36 |
| y2 |
| 12 |
| 3 |
2
| ||
| 6 |
| ||
| 3 |
| 3 |
故选A.
点评:本题考查椭圆的性质与双曲线的性质及标准方程,求得双曲线的焦点是关键,属于中档题.

练习册系列答案
相关题目