题目内容
设函数f（x）=x（x-1）2．
（1）求f（x）在区间[
，2]上的最大值和最小值；
（2）当a≥0时，讨论方程
+x--alnx=0的解的个数，并说明理由．
解：（1）f′（x）=3x2-4x+1，∵f′（x）＞0?x＞1或x＜
，∴f（x）在[，1]上递减，在（1，2]上递增，
∴f（x）min=f（1）=0，又f（）=
，f（2）=2，
∴f（x）max=f（2）=2．
（2）
?
，令g（x）=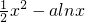
，
则g′（x）=
，
①当a=0时，g（x）=
，则g（x）=0在（0，+∞）上无解；
②当a＞0时，则g（x）在（0，
）上递减，在（，+∞）上递增，
∴
=
-
，
又∵当x→0时，g（x）→+∞；当x→+∞时，g（x）→+∞，∴
（ⅰ）当
＞0即0＜a＜e时，g（x）=0在（0，+∞）上无解；
（ⅱ）当=0即a=e时，g（x）=0在（0，+∞）上有一解；
（ⅲ）当＜0即a＞e时，g（x）=0在（0，+∞）上有两解；
综上：当a＞e时，g（x）=0在（0，+∞）上有两解；当a=e时，g（x）=0在（0，+∞）上有一解；
当0≤a＜e时，g（x）=0在（0，+∞）上无解．
分析：（1）求出函数在区间端点处的函数值，然后用导数求出极值，比较它们的大小，其中最大者为最大值，最小者为最小值；
（2）恰当构造函数，转化为函数零点问题，利用导数研究该函数的单调性及其最值，结合图象即可得到答案．
点评：本题考查利用导数研究函数最值、单调性问题，考查分析问题、解决问题的能力，本题中渗透了分类讨论思想及函数与方程思想．
，∴f（x）在[，1]上递减，在（1，2]上递增，∴f（x）min=f（1）=0，又f（
）=，f（2）=2，∴f（x）max=f（2）=2．
（2）
?，令g（x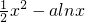）=，则g′（x）=
，①当a=0时，g（x）=
，则g（x）=0在（0，+∞）上无解；②当a＞0时，则g（x）在（0，
）上递减，在（，+∞）上递增，∴
=-，又∵当x→0时，g（x）→+∞；当x→+∞时，g（x）→+∞，∴
（ⅰ）当
＞0即0＜a＜e时，g（x）=0在（0，+∞）上无解；（ⅱ）当
=0即a=e时，g（x）=0在（0，+∞）上有一解；（ⅲ）当
＜0即a＞e时，g（x）=0在（0，+∞）上有两解； 综上：当a＞e时，g（x）=0在（0，+∞）上有两解；当a=e时，g（x）=0在（0，+∞）上有一解；
当0≤a＜e时，g（x）=0在（0，+∞）上无解．
分析：（1）求出函数在区间端点处的函数值，然后用导数求出极值，比较它们的大小，其中最大者为最大值，最小者为最小值；
（2）恰当构造函数，转化为函数零点问题，利用导数研究该函数的单调性及其最值，结合图象即可得到答案．
点评：本题考查利用导数研究函数最值、单调性问题，考查分析问题、解决问题的能力，本题中渗透了分类讨论思想及函数与方程思想．
练习册系列答案
相关题目
设函数f（x）的定义域为A，若存在非零实数t，使得对于任意x∈C（C⊆A），有x+t∈A，且f（x+t）≤f（x），则称f（x）为C上的t低调函数．如果定义域为[0，+∞）的函数f（x）=-|x-m2|+m2，且 f（x）为[0，+∞）上的10低调函数，那么实数m的取值范围是（ ）
| A、[-5，5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|