题目内容
已知椭圆C: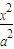 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点O为圆心,以椭圆的短半轴长为半径的圆与直线x-y+
,以原点O为圆心,以椭圆的短半轴长为半径的圆与直线x-y+ =0相切;若直线l:y=kx+m与椭圆C相交于A,B两点.直线OA和OB的斜率分别为kOA和kOB,且kOA•kOB=-
=0相切;若直线l:y=kx+m与椭圆C相交于A,B两点.直线OA和OB的斜率分别为kOA和kOB,且kOA•kOB=-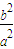 .
.(1)求椭圆C的方程;
(2)求证:△OAB的面积为定值.
【答案】分析:(1)由椭圆的离心率为 ,圆心到直线x-y+
,圆心到直线x-y+ =0的距离等于b及c2=a2-b2联立方程组求解a2,b2,则椭圆的方程可求;
=0的距离等于b及c2=a2-b2联立方程组求解a2,b2,则椭圆的方程可求;
(2)把直线l的方程和椭圆方程联立,利用根与系数的关系求出直线和椭圆两个交点的横坐标的和与积,代入直线方程求出两交点的纵坐标的积,结合kOA•kOB=- 得到k与m的关系,借助于弦长公式求出|AB|的长度,由点到直线的距离公式求出O到直线y=kx+m的距离,写出三角形AOB的面积后转化为含有k的代数式,整理后得到结果为定值.
得到k与m的关系,借助于弦长公式求出|AB|的长度,由点到直线的距离公式求出O到直线y=kx+m的距离,写出三角形AOB的面积后转化为含有k的代数式,整理后得到结果为定值.
解答:(1)解:由题意得 ,解得a2=4,b2=3.
,解得a2=4,b2=3.
所以椭圆的方程为 ;
;
(2)证明:设A(x1,y1),(x2,y2),则A,B的坐标满足 ,
,
整理得,(3+4k2)x2+8kmx+4m2-12=0.
∴ ,
, .
.
由△>0,得4k2-m2+3>0.
y1y2=(kx1+m)(kx2+m)=
= =
= .
.
∵ ,∴
,∴ ,即
,即 ,
,
∴ ,即2m2-4k2=3.
,即2m2-4k2=3.
∵ =
=
= .
.
O到直线y=kx+m的距离d= ,
,
∴
= =
= .为定值.
.为定值.
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题.
 ,圆心到直线x-y+
,圆心到直线x-y+ =0的距离等于b及c2=a2-b2联立方程组求解a2,b2,则椭圆的方程可求;
=0的距离等于b及c2=a2-b2联立方程组求解a2,b2,则椭圆的方程可求;(2)把直线l的方程和椭圆方程联立,利用根与系数的关系求出直线和椭圆两个交点的横坐标的和与积,代入直线方程求出两交点的纵坐标的积,结合kOA•kOB=-
 得到k与m的关系,借助于弦长公式求出|AB|的长度,由点到直线的距离公式求出O到直线y=kx+m的距离,写出三角形AOB的面积后转化为含有k的代数式,整理后得到结果为定值.
得到k与m的关系,借助于弦长公式求出|AB|的长度,由点到直线的距离公式求出O到直线y=kx+m的距离,写出三角形AOB的面积后转化为含有k的代数式,整理后得到结果为定值.解答:(1)解:由题意得
 ,解得a2=4,b2=3.
,解得a2=4,b2=3.所以椭圆的方程为
 ;
;(2)证明:设A(x1,y1),(x2,y2),则A,B的坐标满足
 ,
,整理得,(3+4k2)x2+8kmx+4m2-12=0.
∴
 ,
, .
.由△>0,得4k2-m2+3>0.
y1y2=(kx1+m)(kx2+m)=

=
 =
= .
.∵
 ,∴
,∴ ,即
,即 ,
,∴
 ,即2m2-4k2=3.
,即2m2-4k2=3.∵
 =
=
=
 .
.O到直线y=kx+m的距离d=
 ,
,∴

=
 =
= .为定值.
.为定值.点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为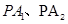 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.