题目内容
设 ,函数f(x)的定义域为[0,1],且f(0)=0,f(1)=1,当x≥y时,
,函数f(x)的定义域为[0,1],且f(0)=0,f(1)=1,当x≥y时, .
.
(Ⅰ)求 ,
,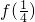 ;
;
(Ⅱ)求α的值;
(Ⅲ)求 的单调增区间.
的单调增区间.
解:(Ⅰ)令x=1,y=0,
令 ,y=0,
,y=0, .
.
(Ⅱ)令x=1,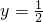 ,
,
=sinα+(1-sinα)sinα
=-sin2α+2sinα.
令 ,
,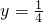 ,
,
∴-2sin3α+3sin2α=sinα
∴
∵
∴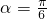 ;
;
(Ⅲ)
=
要使g(x)单调增区间,
则
∴单调增区间是: .
.
分析:(Ⅰ)令x=1,y=0代入到 可求得
可求得 的值,令
的值,令 ,y=0代入到
,y=0代入到 可求得
可求得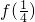 的值.
的值.
(Ⅱ)先令x=1,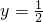 代入到
代入到 可表示出f(
可表示出f( ),然后令
),然后令 ,
,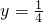 和f(
和f( )的值代入到
)的值代入到 中,即可得到
中,即可得到 ,再结合α的范围可求得到答案.
,再结合α的范围可求得到答案.
(Ⅲ)先将α的值代入根据两角和与差的公式进行化简,再根据正弦函数的单调性可得到单调增区间.
点评:本题主要考查两角和与差的公式的应用和正弦函数的单调性.考查考生对基础知识的综合应用能力和计算能力,三角函数的公式记忆是学习三角函数的难点,平时一定要注意积累.

令
 ,y=0,
,y=0, .
.(Ⅱ)令x=1,
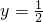 ,
,
=sinα+(1-sinα)sinα
=-sin2α+2sinα.
令
 ,
,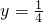 ,
,
∴-2sin3α+3sin2α=sinα
∴

∵

∴
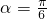 ;
;(Ⅲ)

=

要使g(x)单调增区间,
则

∴单调增区间是:
 .
.分析:(Ⅰ)令x=1,y=0代入到
 可求得
可求得 的值,令
的值,令 ,y=0代入到
,y=0代入到 可求得
可求得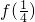 的值.
的值.(Ⅱ)先令x=1,
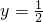 代入到
代入到 可表示出f(
可表示出f( ),然后令
),然后令 ,
,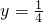 和f(
和f( )的值代入到
)的值代入到 中,即可得到
中,即可得到 ,再结合α的范围可求得到答案.
,再结合α的范围可求得到答案.(Ⅲ)先将α的值代入根据两角和与差的公式进行化简,再根据正弦函数的单调性可得到单调增区间.
点评:本题主要考查两角和与差的公式的应用和正弦函数的单调性.考查考生对基础知识的综合应用能力和计算能力,三角函数的公式记忆是学习三角函数的难点,平时一定要注意积累.

练习册系列答案
相关题目
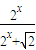 的图象上两点P1(x1,y1) P2(x2,y2),若
的图象上两点P1(x1,y1) P2(x2,y2),若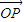 =
= (
(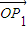 +
+ ),且点P的横坐标为
),且点P的横坐标为 (1)求证:P点的纵坐标为定值,并求出这个定值;(2)若Sn=
(1)求证:P点的纵坐标为定值,并求出这个定值;(2)若Sn=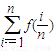 ,n∈N*,求Sn;
,n∈N*,求Sn;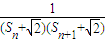 }的前n项和,若Tn<a(
}的前n项和,若Tn<a(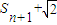 )对一切n∈N*都成立,试求a的取值范围
)对一切n∈N*都成立,试求a的取值范围