题目内容
已知函数 ,
, 。
。
(1)设函数F(x)=f(x)-h(x),求F(x)的单调区间与极值;
(2)设a∈R,解关于x的方程 ;
;
(3)试比较f(100)h(100)- 与
与 的大小。
的大小。
 ,
, 。
。(1)设函数F(x)=f(x)-h(x),求F(x)的单调区间与极值;
(2)设a∈R,解关于x的方程
 ;
;(3)试比较f(100)h(100)-
 与
与 的大小。
的大小。解:(1)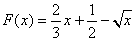
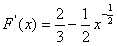
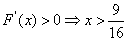
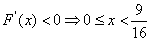
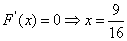
所以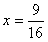 是其极小值点,极小值为
是其极小值点,极小值为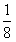 ;x=0是其极大值点,极大值为
;x=0是其极大值点,极大值为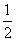 ;
;
(2)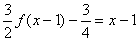
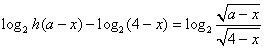
由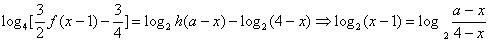
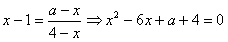
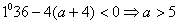 时方程无解
时方程无解
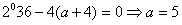 时x=3
时x=3
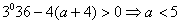 方程的根为
方程的根为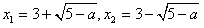 ;
;
(3)设数列{an}的前n项和为Sn,且Sn=f(n)g(n)-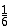
从而有a1=S1=1
当2<k≤100时,ak=Sk-Sk-1=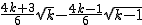
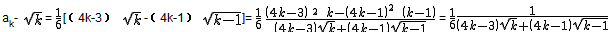 >0
>0
即对任意的2<k≤100,都有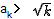
又因为a1=S1=1
所以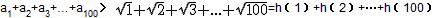
故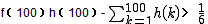 。
。
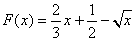
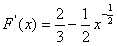
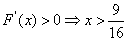
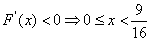
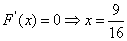
所以
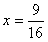 是其极小值点,极小值为
是其极小值点,极小值为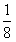 ;x=0是其极大值点,极大值为
;x=0是其极大值点,极大值为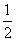 ;
;(2)
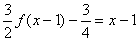
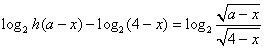
由
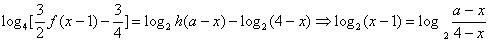
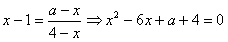
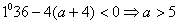 时方程无解
时方程无解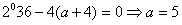 时x=3
时x=3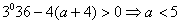 方程的根为
方程的根为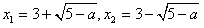 ;
;(3)设数列{an}的前n项和为Sn,且Sn=f(n)g(n)-
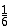
从而有a1=S1=1
当2<k≤100时,ak=Sk-Sk-1=
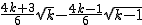
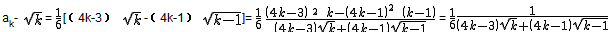 >0
>0即对任意的2<k≤100,都有
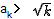
又因为a1=S1=1
所以
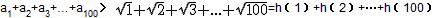
故
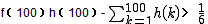 。
。
练习册系列答案
相关题目
已知函数f(x)=-
,设an=
,若-1≤x1<0<x2<x3,则( )
| x+1 |
| f(xn)-2 |
| xn |
| A、a2<a3<a1 |
| B、a1<a2<a3 |
| C、a1<a3<a2 |
| D、a3<a2<a1 |
 ,
, .
. ,
, .
. 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值;
的值; 的单调递增区间.
的单调递增区间. ,其中
,其中
 ,若
,若 在区间
在区间 上不是单调函数,求
上不是单调函数,求 的取值范围.
的取值范围.
 是否存在
是否存在 ,存在唯一的非零实数
,存在唯一的非零实数 使得
使得 成立,若存在,求
成立,若存在,求 ,
, .
. 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值;
的值; 的单调递增区间.
的单调递增区间.