题目内容

函数f（x）=x（1-x²）在[0，1]上的最大值为

A.
$数学公式$
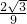
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

A
分析：求出函数的导函数，令导函数为求出根，判断根左右两边的导函数符号，判断出函数的单调性，求出函数的最大值．
解答：∵f（x）=x-x³
∴f′（x）=1-3x²
令f′（x）=0得 $\text{[math]}$
$\text{[math]}$ ； $\text{[math]}$
所以当 $\text{[math]}$ $\text{[math]}$
故答案为A
点评：求函数在给定区间上的最值问题，应该先通过求导函数判断出函数的单调性，求出函数的极值，再求出区间端点对应的函数值，从中选出最值．

练习册系列答案

细解巧练系列答案

高效学案金典课堂系列答案

一线课堂导学案系列答案

走向中考考场系列答案

新编能力拓展练习系列答案

练案系列答案

金榜行动系列答案

学习质量监测系列答案

海淀单元测试AB卷系列答案

金阶梯课课练单元测系列答案

相关题目

设函数f（x）=a²x²（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为

，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=

，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

（2012•深圳一模）已知函数f(x)=

x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x

， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．

若函数f（x）是奇函数，当x＜0时，f（x）的解析式是f（x）=x（1-x），则当x＞0时，的解析式是

A.
f（x）=-x（1-x）
B.
f（x）=x（1-x）
C.
f（x）=-x（1+x）
D.
f（x）=x（1+x）

已知函数f(x)=

x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x

， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．

设函数f（x）=a²x²（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2

，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=

，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．