题目内容
20.已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{\sqrt{2}}{2}$,且椭圆上点到椭圆C1左焦点距离的最小值为$\sqrt{2}$-1.(1)求C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
分析 (1)运用椭圆的离心率和最小距离a-c,解方程可得a=$\sqrt{2}$,c=1,再由a,b,c的关系,可得b,进而得到椭圆方程;
(2)设出直线y=kx+m,联立椭圆和抛物线方程,运用判别式为0,解方程可得k,m,进而得到所求直线的方程.
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
由椭圆的性质可得,a-c=$\sqrt{2}$-1,
解方程可得a=$\sqrt{2}$,c=1,
则b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
即有椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)直线l的斜率显然存在,可设直线l:y=kx+m,
由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,可得(1+2k2)x2+4kmx+2m2-2=0,
由直线和椭圆相切,可得△=16k2m2-4(1+2k2)(2m2-2)=0,
即为m2=1+2k2,①
由$\left\{\begin{array}{l}{y=kx+m}\\{{y}^{2}=4x}\end{array}\right.$,可得k2x2+(2km-4)x+m2=0,
由直线和抛物线相切,可得△=(2km-4)2-4k2m2=0,
即为km=1,②
由①②可得$\left\{\begin{array}{l}{k=\frac{\sqrt{2}}{2}}\\{m=\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{k=-\frac{\sqrt{2}}{2}}\\{m=-\sqrt{2}}\end{array}\right.$,
即有直线l的方程为y=$\frac{\sqrt{2}}{2}$x+$\sqrt{2}$或y=-$\frac{\sqrt{2}}{2}$x-$\sqrt{2}$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质:离心率和最小距离a-c,考查直线方程的求法,注意运用联立直线方程和曲线方程,运用判别式为0,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
| A. | ${log_{0.2}}3<{e^{-\sqrt{2}}}<{({a^2}+3)^0}<lnπ$ | B. | ${e^{-\sqrt{2}}}<{log_{0.2}}3<{({a^2}+3)^0}<lnπ$ | ||
| C. | ${e^{-\sqrt{2}}}<{({a^2}+3)^0}<{log_{0.2}}3<lnπ$ | D. | ${log_{0.2}}3<{({a^2}+3)^0}<{e^{-\sqrt{2}}}<lnπ$ |
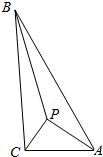 如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.
如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.