题目内容
如图，已知△ABC是边长为1的正三角形，M、N分别是边AB、AC上的点，线段MN经过△ABC的中心G，设∠MGA=a（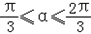
）
（1）试将△AGM、△AGN的面积（分别记为S1与S2）表示为a的函数．
（2）求y=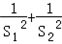
的最大值与最小值．
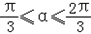）（1）试将△AGM、△AGN的面积（分别记为S1与S2）表示为a的函数．
（2）求y=
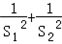的最大值与最小值．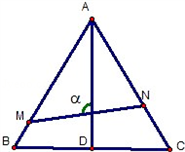
解：（1）因为G是边长为1的正三角形ABC的中心，
所以AG=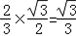
，∠MAG=
，
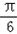由正弦定理
得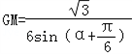
则S1=
GM·GA·sina=
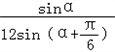
理可求得S2=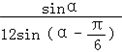
（2）y=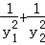
=
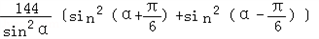
=72（3+cot2a）
因为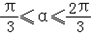
，
所以当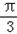a=
或a=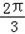
时，y取得最大值ymax=240
当a=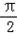
时，y取得最小值ymin=216
所以AG=
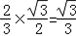，∠MAG=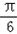，由正弦定理
得
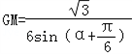
则S1=
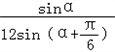
GM·GA·sina=理可求得S2=
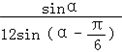
（2）y=
=
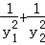
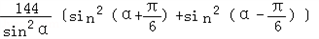
=72（3+cot2a）
因为
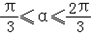，所以当a=
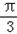或a=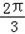时，y取得最大值ymax=240当a=
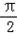时，y取得最小值ymin=216
练习册系列答案
相关题目
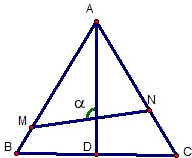如图，已知△ABC是边长为1的正三角形，M、N分别是边AB、AC上的点，线段MN经过△ABC的中心G，设?MGA=a（
20、如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BE的中点．
如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BE的中点，求证：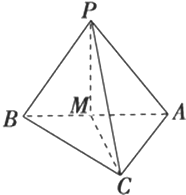
如图：已知△ABC是直角三角形，∠ACB=90°，M为AB的中点，PM⊥△ABC所在的平面，那么PA、PB、PC的大小关系是（ ）