题目内容
已知函数f(α)=
．
（1）若角α为第一象限角，且cosα=
，求f（α）；
（2）若tanα=2，求f2（α）．
1+
| ||||
sin(α+
|
（1）若角α为第一象限角，且cosα=
| 3 |
| 5 |
（2）若tanα=2，求f2（α）．
分析：先利用两角差的余弦公式和诱导公式、倍角公式将已知函数化简单角α的三角函数式，（1）先利用同角三角函数基本关系式计算sinα的值，再代入函数解析式即可；（2）先利用同角三角函数基本关系式、二倍角公式将f2（α）化简为关于tanα的三角函数式，最后将已知代入求值即可
解答：解：f(α)=
=
=
=
=
（1）∵α为第一象限角，且cosα=
，
∴sinα=
∴f（α）=
=
=
（2）∵tanα=2
∴f2（α）=
=4tan2α×
=4tan2α×
=4×4×
=
1+
| ||||
sin(α+
|
1+
| ||||||||||
| cosα |
| 1+cos2α+sin2α |
| cosα |
| 2sin2α+2sinαcosα |
| cosα |
| 2sinα(sinα+cosα) |
| cosα |
（1）∵α为第一象限角，且cosα=
| 3 |
| 5 |
∴sinα=
| 4 |
| 5 |
∴f（α）=
| 2sinα(sinα+cosα) |
| cosα |
2×
| ||||||
|
| 56 |
| 15 |
（2）∵tanα=2
∴f2（α）=
| 4sin2α(sinα+cosα) 2 |
| cos2α |
| sin2α +cos2α+2sinαcosα |
| sin2α+cos2α |
| tan2α + 1+2tanα |
| tan2α+1 |
| 4+1+4 |
| 4+1 |
| 144 |
| 5 |
点评：本题主要考查了利用两角差的余弦公式和诱导公式、倍角公式进行化简和求值的能力，整体代入的思想方法
练习册系列答案
相关题目
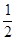, f'(x)是f(x)的导函数,若
x∈R,
f'(x)<ex ,则不等式f(x)<ex-