Question

【题目】已知点A（0，2），B（4，6）， =t1 +t2 ，其中t1、t2为实数；
（1）若点M在第二或第三象限，且t1=2，求t2的取值范围；
（2）求证：当t1=1时，不论t2为何值，A、B、M三点共线；
（3）若t1=a2 ， ⊥ ，且△ABM的面积为12，求a和t2的值．

Answer 1

【答案】
（1）解：由A（0，2），B（4，6），

得 =（4，4），

∴ =t1 +t2 =（4t2，2t1+4t2），

又点M在第二象限或第三象限，

∴ ，

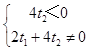又t1=2，

解得t2＜0且t2≠﹣1，

∴t2的取值范围是（﹣∞，﹣1）∪（﹣1，0）

（2）证明：t1=1时，

=t1 +t2 = +t2 ，

∴ ﹣ =t2 ，

即 =t2 ，

∴不论t2为何值，A、B、M三点共线

（3）解：∵当t1=a2时， =（4t2，4t2+2a2），

又∵ =（4，4）， ⊥ ，

∴4t2×4+（4t2+2a2）×4=0，

∴t2=﹣ a2．

∴ =（﹣a2，a2）；

又∵| |=4 ，

点M到直线AB：x﹣y+2=0的距离为

d= = |a2﹣1|；

∵S△ABM=12，

∴ | |d= ×4 × |a2﹣1|=12，

解得a=±2，此时t2=﹣ a2=﹣1

【解析】（1）由题设条件，得 =（4t2 ， 2t1+4t2），又点M在第二象限或第三象限，列出不等式求出t2的取值范围；（2）由平面向量的共线定理，得 =t2 ，能证明A，B，M三点共线；（3）由t1=a2表示出 、 ，利用 ⊥ 求出t2=﹣ a2 ， 再由S△ABM=12求出a的值和t2的值．
【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点，需要掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使才能正确解答此题．