题目内容
已知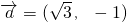 ,
,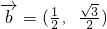
(Ⅰ)若存在实数k和t,使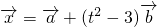 ,
,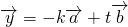 ,且
,且 ⊥
⊥ ,试求函数关系式k=f(t);
,试求函数关系式k=f(t);
(Ⅱ)根据(Ⅰ)的结论,确定k=f(t)的单调区间;
(Ⅲ)设a>0,若过点(a,b)可作曲线k=f(t)的三条切线,求证: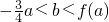 .
.
解:(Ⅰ)∵知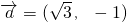 ,
,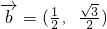 ,
,
∴ =0,|
=0,| |=
|= =2,|
=2,| |=
|= =1,
=1,
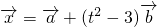 =(
=(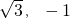 )+(
)+( ,
, )=(
)=( ,
, ),
),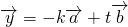 =(-
=(- )+(
)+( )=(
)=( ,
, ),
),
∴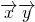 =-4k+t(t2-3)=0,
=-4k+t(t2-3)=0,
∴k=f(t)= .
.
(Ⅱ)∵f(t)= ,
,
∴f′(x)=k′= =
= ,
,
令k′>0,得t>1,或t<-1,
令k′<0,得-1<t<1,
∴k=f(t)的单调增区间为(1,+∞),(-∞,-1);单调减区间为(-1,1).
(Ⅲ)设切点为(t, ),
), ,
,
∴切线方程为:y- ,
,
∵切线方程过(a,b),
∴b- =
= ,
,
4b-t3+3t=(3t2-3)(a-t),
4b-t3+3t=3at2-3t2-3a+3t,
∴3a+4b=-2t3+3at2有三个不同的根,
令g(t)=-2t3+3at2,
g′(t)=-6t2+6at=-6t(t-a),
令g′(t)=0,得t=0,或t=a.
令g′(t)>0,得0<t<a,
令g′(x)<0,得t>a,或t<0,
∴g(t)极小值=g(0)=0,
g(t)极大值=g(a)=a3,
∴要使3a+4b=-2t3+3at2有三个不同的根,
则0<3a+4b<a3,
∴ ,
,
故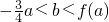 .
.
分析:(Ⅰ)由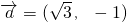 ,
,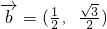 ,知
,知 =0,|
=0,| |=2,|
|=2,| |=1,由此能求出k=f(t).
|=1,由此能求出k=f(t).
(Ⅱ)由f(t)= ,知f′(x)=k′=
,知f′(x)=k′= =
= ,由此能求出k=f(t)的单调区间.
,由此能求出k=f(t)的单调区间.
(Ⅲ)设切点为(t, ),
), ,则切线方程为:y-
,则切线方程为:y- ,由切线方程过(a,b),知b-
,由切线方程过(a,b),知b- =
= ,由此能够证明
,由此能够证明
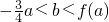 .
.
点评:本题考查数量积判断两个平面向量垂直的条件的应用,具体涉及到平面向量的性质、导数的应用、函数性质、切线方程等基本知识点,解题时要认真审题,仔细解答.
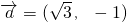 ,
,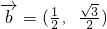 ,
,∴
 =0,|
=0,| |=
|= =2,|
=2,| |=
|= =1,
=1,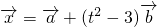 =(
=(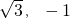 )+(
)+( ,
, )=(
)=( ,
, ),
),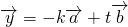 =(-
=(- )+(
)+( )=(
)=( ,
, ),
),∴
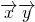 =-4k+t(t2-3)=0,
=-4k+t(t2-3)=0,∴k=f(t)=
 .
.(Ⅱ)∵f(t)=
 ,
,∴f′(x)=k′=
 =
= ,
,令k′>0,得t>1,或t<-1,
令k′<0,得-1<t<1,
∴k=f(t)的单调增区间为(1,+∞),(-∞,-1);单调减区间为(-1,1).
(Ⅲ)设切点为(t,
 ),
), ,
,∴切线方程为:y-
 ,
,∵切线方程过(a,b),
∴b-
 =
= ,
,4b-t3+3t=(3t2-3)(a-t),
4b-t3+3t=3at2-3t2-3a+3t,
∴3a+4b=-2t3+3at2有三个不同的根,
令g(t)=-2t3+3at2,
g′(t)=-6t2+6at=-6t(t-a),
令g′(t)=0,得t=0,或t=a.
令g′(t)>0,得0<t<a,
令g′(x)<0,得t>a,或t<0,
∴g(t)极小值=g(0)=0,
g(t)极大值=g(a)=a3,
∴要使3a+4b=-2t3+3at2有三个不同的根,
则0<3a+4b<a3,
∴
 ,
,故
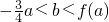 .
.分析:(Ⅰ)由
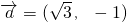 ,
,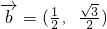 ,知
,知 =0,|
=0,| |=2,|
|=2,| |=1,由此能求出k=f(t).
|=1,由此能求出k=f(t).(Ⅱ)由f(t)=
 ,知f′(x)=k′=
,知f′(x)=k′= =
= ,由此能求出k=f(t)的单调区间.
,由此能求出k=f(t)的单调区间.(Ⅲ)设切点为(t,
 ),
), ,则切线方程为:y-
,则切线方程为:y- ,由切线方程过(a,b),知b-
,由切线方程过(a,b),知b- =
= ,由此能够证明
,由此能够证明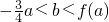 .
.点评:本题考查数量积判断两个平面向量垂直的条件的应用,具体涉及到平面向量的性质、导数的应用、函数性质、切线方程等基本知识点,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 和点M满足
和点M满足 .若存在实
.若存在实 使得
使得 成立,则
成立,则 和点M满足
和点M满足 .若存在实
.若存在实 使得
使得 成立,则
成立,则