题目内容
【题目】已知![]() ,
,![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个不等的实根,且
的两个不等的实根,且![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,记
,记![]() ,
,![]() 分别为函数
分别为函数![]() 的最大值和最小值.
的最大值和最小值.
(1)试判断![]() 在
在![]() 上的单调性;
上的单调性;
(2)设![]() ,若函数
,若函数![]() 是奇函数,求实数
是奇函数,求实数![]() 的值.
的值.
【答案】(1)函数![]() 在
在![]() 上单调递增;(2)
上单调递增;(2)![]() .
.
【解析】
(1)利用函数单调性的定义或利用导数判断![]() 在
在![]() 上的单调性;
上的单调性;
(2)由(1)可知函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,![]() ,求出
,求出![]() .由
.由![]() 是奇函数,可得
是奇函数,可得![]() ,即求
,即求![]() .
.
(1)解法一:对于![]() ,
,![]() ,设
,设![]()
则 ,
,
 ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
解法二:设![]() ,
, ,
,
因为![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个不等的实根,
的两个不等的实根,
所以![]() ,
,
所以![]() ,等号当且仅当
,等号当且仅当![]() 或
或![]() 时成立,
时成立,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
(2)由(1)可知函数![]() 在
在![]() 上是单调递增的,
上是单调递增的,
所以![]() ,
,![]() ,
,
所以 ,
,
因为![]() ,
,![]() 为方程
为方程![]() 的两个实根,
的两个实根,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() 是奇函数,所以
是奇函数,所以![]() 对任意
对任意![]() 都成立,
都成立,
即![]() 恒成立,
恒成立,
![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以![]() ,即
,即![]() .
.

【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每个人每日健步的步数,从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况,从本市市民中随机抽取了2000名市民(其中不超过40岁的市民恰好有1000名),利用手机计步软件统计了他们某天健步的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
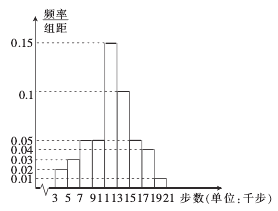
,![]() 九组(单位:千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如右,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
九组(单位:千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如右,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
分组 (单位:千步) |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
(1)现规定,日健步步数不低于13000步的为“健步达人”,填写下面列联表,并根据列联表判断能否有![]() %的把握认为是否为“健步达人”与年龄有关;
%的把握认为是否为“健步达人”与年龄有关;
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
(2)(ⅰ)利用样本平均数和中位数估计该市不超过40岁的市民日健步步数(单位:千步)的平均数和中位数;
(ⅱ)由频率分布直方图可以认为,不超过40岁的市民日健步步数![]() (单位:千步)近似地服从正态分布
(单位:千步)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值),
(每组数据取区间的中点值),![]() 的值已求出约为
的值已求出约为![]() .现从该市不超过40岁的市民中随机抽取5人,记其中日健步步数
.现从该市不超过40岁的市民中随机抽取5人,记其中日健步步数![]() 位于
位于![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
参考公式: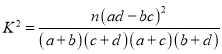 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
若![]() ,则
,则![]() ,
,![]() .
.