题目内容
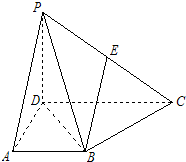 在四棱锥P-ABCD中,PD⊥底面ABCD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=1,CD=2.
(1)求证:BE∥平面PAD;
(2)求证:BC⊥平面PBD;
(3)若直线PB与底面ABCD所成角为45°,求线段PD的长(此问只需写出答案,无需写过程).
解:(1)取PD的中点F,连结EF,AF,
∵E为PC中点,∴EF∥CD,且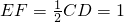 ,
,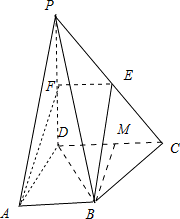
在梯形ABCD中,AB∥CD,AB=1,∴EF∥AB,EF=AB,
四边形ABEF为平行四边形,∴BE∥AF,
∵BE?平面PAD,AF?平面PAD,
∴BE∥平面PAD.
(2)取CD中点M,连结BM,可知△BMC为直角三角形且BM=MC=1,∴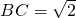 ,
,
在△ABD中,可知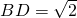 ,∴CD2=BD2+BC2,∴BC⊥BD.
,∴CD2=BD2+BC2,∴BC⊥BD.
又由PD⊥平面ABCD,可得PD⊥BC,
又PD∩BD=D,
∴BC⊥平面PBD.
(3)∵PD⊥底面ABCD,∴∠PBD是斜线PB与平面ABCD所成的线面角.
可知∠PBD=45°,由(2)可知:BD= .
.
∴PD=BD= .
.
分析:(1)利用三角形的中位线定理EF∥CD且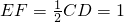 ,由平行四边形的判定可得平行四边形ABEF,由性质定理可得BE∥AF,再利用线面平行的判定定理即可证明;
,由平行四边形的判定可得平行四边形ABEF,由性质定理可得BE∥AF,再利用线面平行的判定定理即可证明;
(2)取CD中点M,连结BM,则四边形ABMD为正方形,可得BD,BC的长,利用勾股定理的逆定理即可判断BC⊥BD,再利用线面垂直的性质定理即可得出PD⊥BC,再利用线面垂直的判定定理即可证明;
(3)利用线面角的定义及等腰直角三角形的性质即可得出.
点评:熟练掌握三角形的中位线定理、平行四边形的判定和性质定理、线面平行的判定定理、正方形的判定与性质、勾股定理的逆定理、线面垂直的判定定理和性质定理、线面角的定义及等腰直角三角形的性质是解题的关键.
∵E为PC中点,∴EF∥CD,且
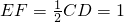 ,
,
在梯形ABCD中,AB∥CD,AB=1,∴EF∥AB,EF=AB,
四边形ABEF为平行四边形,∴BE∥AF,
∵BE?平面PAD,AF?平面PAD,
∴BE∥平面PAD.
(2)取CD中点M,连结BM,可知△BMC为直角三角形且BM=MC=1,∴
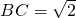 ,
,在△ABD中,可知
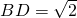 ,∴CD2=BD2+BC2,∴BC⊥BD.
,∴CD2=BD2+BC2,∴BC⊥BD.又由PD⊥平面ABCD,可得PD⊥BC,
又PD∩BD=D,
∴BC⊥平面PBD.
(3)∵PD⊥底面ABCD,∴∠PBD是斜线PB与平面ABCD所成的线面角.
可知∠PBD=45°,由(2)可知:BD=
 .
.∴PD=BD=
 .
.分析:(1)利用三角形的中位线定理EF∥CD且
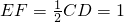 ,由平行四边形的判定可得平行四边形ABEF,由性质定理可得BE∥AF,再利用线面平行的判定定理即可证明;
,由平行四边形的判定可得平行四边形ABEF,由性质定理可得BE∥AF,再利用线面平行的判定定理即可证明;(2)取CD中点M,连结BM,则四边形ABMD为正方形,可得BD,BC的长,利用勾股定理的逆定理即可判断BC⊥BD,再利用线面垂直的性质定理即可得出PD⊥BC,再利用线面垂直的判定定理即可证明;
(3)利用线面角的定义及等腰直角三角形的性质即可得出.
点评:熟练掌握三角形的中位线定理、平行四边形的判定和性质定理、线面平行的判定定理、正方形的判定与性质、勾股定理的逆定理、线面垂直的判定定理和性质定理、线面角的定义及等腰直角三角形的性质是解题的关键.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,