题目内容
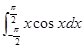的值为 （ ）
| A．0 | B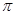． | C．2 | D．-2 |
A
解析试题分析：函数
，当
时有
，所以函数是奇函数图像关于
对称，因此与x轴围成的图形关于原点是对称的，即x轴上方和下方的面积相等，又图像在x轴上方时面积值等于定积分，在下方时面积等于定积分的相反数，结合定积分的几何意义可知定积分值为0
考点：函数性质及定积分的几何意义
点评：本题求定积分值时，被积函数的原函数不易求出，因此结合图像与定积分的几何意义求解，当函数图像在x轴上方时，定积分值等于围成的图形的面积，当函数图象在x轴下方时，定积分值与面积互为相反数
练习册系列答案
相关题目
“
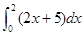等于
| A．9 | B．11 | C．14 | D．18 |
曲线y＝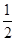
x2－2x在点
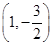处的切线的倾斜角为( )．
| A．－135° | B．45° | C．－45° | D．135° |
若函数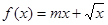
在区间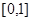
单调递增，则m的取值范围为
A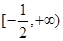． | B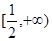． | C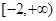． | D． |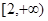
积分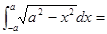
（ ）
A． | B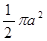． | C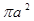． | D． |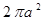
在曲线y＝x3＋x－2的切线中，与直线4x-y＝1平行的切线方程是( )
| A．4x－y＝0 | B．4x－y－4＝0 | C．2x－y－2＝0 | D．4x－y＝0或4x－y－4＝0 |
已知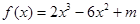
（
为常数）在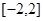
上有最大值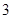
，那么此函数在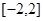上的最小值为（ ）
| A．-37 | B．-29 | C．-5 | D．-11 |
函数y=x2cosx的导数为（ ）.
| A．y′=2xcosx－x2sinx | B．y′=2xcosx+x2sinx |
| C． y′=x2cosx－2xsinx | D．y′=xcosx－x2sinx |
是定义域为R的奇函数，且
，
的图象如图所示。若正数
满足
，则
的取值范围是（ ）
