题目内容
正三棱锥的相邻两侧面所成的角为α，则α的取值范围（ ）
分析：如图所示：过A作AD⊥PB于点D，连接DC，可证∠ADC即为侧面PAB与侧面PCB的平面角，设AB=a，AD=b，则b＜a，利用余弦定理通过放缩可求cos∠ADC的范围，从而可求
∠ADC的范围．
∠ADC的范围．
解答：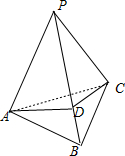
解：如图所示：过A作AD⊥PB于点D，连接DC，
易知△PAB≌△PCB，所以CD⊥PB，
则∠ADC即为侧面PAB与侧面PCB的平面角，
设AB=a，AD=b，则b＜a，
在△ACD中，由余弦定理得，cos∠ADC=
=
＜
=
，
所以∠ADC＞
，即∠ADC的范围为（
，π），
故选B．
解：如图所示：过A作AD⊥PB于点D，连接DC，易知△PAB≌△PCB，所以CD⊥PB，
则∠ADC即为侧面PAB与侧面PCB的平面角，
设AB=a，AD=b，则b＜a，
在△ACD中，由余弦定理得，cos∠ADC=
| AD2+CD2-AC2 |
| 2AD•CD |
| b2+b2-a2 |
| 2b2 |
| b2+b2-b2 |
| 2b2 |
| 1 |
| 2 |
所以∠ADC＞
| π |
| 3 |
| π |
| 3 |
故选B．
点评：本题考查空间中二面角的范围，考查学生的推理论证能力，属中档题．
练习册系列答案
相关题目
) C.(
,
) D.(
,π)