题目内容
已知数列{an}的前n项和Sn=pn+q(p≠0且p≠1),求证:数列{an}为等比数列的充要条件为q=-1.
证明:充分性:当q=-1时,a1=S1=p+q=p-1.
当n≥2时,an=Sn-Sn-1=pn-1(p-1).
当n=1时也成立.
于是
=
=p(n∈N+),
即数列{an}为等比数列.
必要性:当n=1时,a1=S1=p+q.
当n≥2时,an=Sn-Sn-1=pn-1(p-1).
∵p≠0,p≠1.
∴
=
=p.
∵{an}为等比数列,
∴
=
=p,
=p,
即p-1=p+q.∴q=-1.
综上所述,q=-1是数列{an}为等比数列的充要条件.
当n≥2时,an=Sn-Sn-1=pn-1(p-1).
当n=1时也成立.
于是
| an+1 |
| an |
| pn(p-1) |
| pn-1(p-1) |
即数列{an}为等比数列.
必要性:当n=1时,a1=S1=p+q.
当n≥2时,an=Sn-Sn-1=pn-1(p-1).
∵p≠0,p≠1.
∴
| an+1 |
| an |
| pn(p-1) |
| pn-1(p-1) |
∵{an}为等比数列,
∴
| a2 |
| a1 |
| an+1 |
| an |
| p(p-1) |
| p+q |
即p-1=p+q.∴q=-1.
综上所述,q=-1是数列{an}为等比数列的充要条件.

练习册系列答案
相关题目
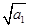 +
+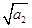 +…+
+…+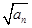 =n2+3n(n∈N*),则
=n2+3n(n∈N*),则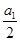 +
+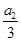 +…+
+…+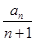 =________.
=________.