题目内容
若数列{an}是正项数列，且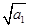
＋
＋…＋
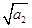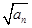＝n2＋3n(n∈N*)，则
＋
＋…＋
＝________.
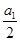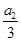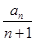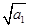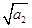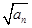＋＋…＋＝n2＋3n(n∈N*)，则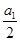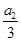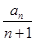＋＋…＋＝________.2n2＋6n
令n＝1，得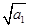＝4，
即a1＝16.
当n≥2时，
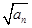＝(n2＋3n)－[(n－1)2＋3(n－1)]＝2n＋2，
所以an＝4(n＋1)2，
当n＝1时，也适合，
所以an＝4(n＋1)2(n∈N*)．
于是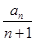＝4(n＋1)，
故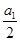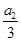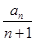＋＋…＋＝2n2＋6n.
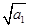＝4，即a1＝16.
当n≥2时，
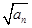＝(n2＋3n)－[(n－1)2＋3(n－1)]＝2n＋2，所以an＝4(n＋1)2，
当n＝1时，也适合，
所以an＝4(n＋1)2(n∈N*)．
于是
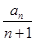＝4(n＋1)，故
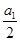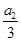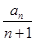＋＋…＋＝2n2＋6n.
练习册系列答案
相关题目
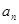
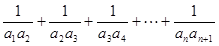
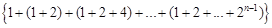的前
项和为_____________.
的通项公式是
,
( )
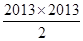
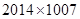
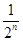，n∈N?，则a3＝________．
，…前n项的和为
