题目内容
已知椭圆C: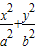 =1(a>b>0)的一个焦点坐标为(1,0),且长轴长是短轴长的
=1(a>b>0)的一个焦点坐标为(1,0),且长轴长是短轴长的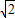 倍.
倍.(Ⅰ)求椭圆C的方程;
(Ⅱ)设O为坐标原点,椭圆C与直线y=kx+1相交于两个不同的点A,B,线段AB的中点为P,若直线OP的斜率为-1,求△OAB的面积.
【答案】分析:(I)先根据题意得关于a,b,c的方程,进而结合椭圆中a,b,c的关系求得a,b,则椭圆方程可得.
(II)设A(0,1),B(x1,y1),P(x,y),联立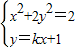 ,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合求根公式,利用弦长公式即可求得k值,从而解决问题.
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合求根公式,利用弦长公式即可求得k值,从而解决问题.
解答:解:(Ⅰ)由题意得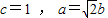 ,(2分)
,(2分)
又a2-b2=1,所以b2=1,a2=2.(3分)
所以椭圆的方程为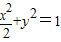 .(4分)
.(4分)
(Ⅱ)设A(0,1),B(x1,y1),P(x,y),
联立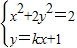 消去y得(1+2k2)x2+4kx=0(*),(6分)
消去y得(1+2k2)x2+4kx=0(*),(6分)
解得x=0或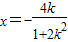 ,所以
,所以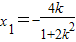 ,
,
所以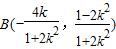 ,
,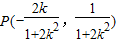 ,(8分)
,(8分)
因为直线OP的斜率为-1,所以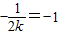 ,
,
解得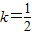 (满足(*)式判别式大于零).(10分)
(满足(*)式判别式大于零).(10分)
O到直线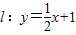 的距离为
的距离为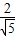 ,(11分)
,(11分)
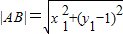 =
=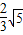 ,(12分)
,(12分)
所以△OAB的面积为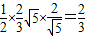 .(13分)
.(13分)
点评:本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线的综合问题是支撑圆锥曲线知识体系的重点内容,问题的解决具有入口宽、方法灵活多样等,而不同的解题途径其运算量繁简差别很大.
(II)设A(0,1),B(x1,y1),P(x,y),联立
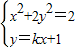 ,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合求根公式,利用弦长公式即可求得k值,从而解决问题.
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合求根公式,利用弦长公式即可求得k值,从而解决问题.解答:解:(Ⅰ)由题意得
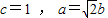 ,(2分)
,(2分)又a2-b2=1,所以b2=1,a2=2.(3分)
所以椭圆的方程为
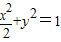 .(4分)
.(4分)(Ⅱ)设A(0,1),B(x1,y1),P(x,y),
联立
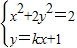 消去y得(1+2k2)x2+4kx=0(*),(6分)
消去y得(1+2k2)x2+4kx=0(*),(6分)解得x=0或
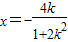 ,所以
,所以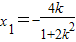 ,
,所以
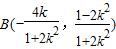 ,
,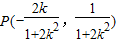 ,(8分)
,(8分)因为直线OP的斜率为-1,所以
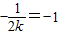 ,
,解得
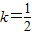 (满足(*)式判别式大于零).(10分)
(满足(*)式判别式大于零).(10分)O到直线
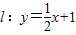 的距离为
的距离为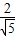 ,(11分)
,(11分)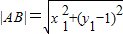 =
=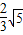 ,(12分)
,(12分)所以△OAB的面积为
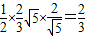 .(13分)
.(13分)点评:本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线的综合问题是支撑圆锥曲线知识体系的重点内容,问题的解决具有入口宽、方法灵活多样等,而不同的解题途径其运算量繁简差别很大.

练习册系列答案
相关题目
 +
+ =1(a>b>0)经过(1,1)与(
=1(a>b>0)经过(1,1)与( ,
, )两点.
)两点. +
+ +
+ 为定值.
为定值.
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.